Altın Oran

Altın oran, doğada sayısız canlının ve cansızın şeklinde ve yapısında bulunan özel bir orandır Doğada bir bütünün parçaları arasında gözlemlenen, yüzyıllarca sanat ve mimaride uygulanmış, uyum açısından en yetkin boyutları verdiği sanılan geometrik ve sayısal bir oran bağıntısıdır Doğada en belirgin örneklerine insan vücudunda, deniz kabuklulularında ve ağaç dallarında rastlanır Platon'a göre kozmik fiziğin anahtarı bu orandır Altın oranı bir dikdörtgenin boyunun enine olan "en estetik" oranı olarak tanımlayanlar da vardır

Eski Mısırlılar ve Yunanlılar tarafından keşfedilmiş, mimaride ve sanatta kullanılmıştır Göze çok hoş gelen bir orandır

Altın Oran; CB / AC = AB / CB = 1618; bu oranın değeri her ölçü için 1618 dir

Bir doğru parçasının (AB) Altın Oran'a uygun biçimde iki parçaya bölünmesi gerektiğinde, bu doğru öyle bir noktadan (C) bölünmelidir ki; küçük parçanın (AC) büyük parçaya (CB) oranı, büyük parçanın (CB) bütün doğruya (AB)oranına eşit olsun

Altın Oran, pi (π) gibi irrasyonel bir sayıdır ve ondalık sistemde yazılışı; 1618033988749894 dür (noktadan sonraki ilk 15 basamak) Bu oranın kısaca gösterimi: 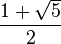olur Altın Oranın ifade edilmesi için kullanılan sembol, PHI yani Φ 'dir

Tarihçe

Altın Oran, matematikte ve fiziksel evrende ezelden beri var olmasına rağmen, insanlar tarafından ne zaman keşfedildiğine ve kullanılmaya başlandığına dair kesin bir bilgi mevcut değildir Tarih boyunca birçok defa yeniden keşfedilmiş olma olasılığı kuvvetlidir

Euclid (MÖ 365 – MÖ 300), "Elementler" adlı tezinde, bir doğruyu 06180399 noktasından bölmekten bahsetmiş ve bunu, bir doğruyu ekstrem ve önemli oranda bölmek diye adlandırmıştır Mısırlılar keops Piramidi'nin tasarımında hem pi hem de phi oranını kullanmışlardır Yunanlılar, Parthenon'un tüm tasarımını Altın Oran'a dayandırmışlardır Bu oran, ünlü Yunanlı heykeltraş Phidias tarafından da kullanılmıştır Leonardo Fibonacci adındaki İtalyan matematikçi, adıyla anılan nümerik serinin olağanüstü özelliklerini keşfetmiştir fakat bunun Altın Oran ile ilişkisini kavrayıp kavramadığı bilinmemektedir Leonardo da Vinci, 1509'da Luca Pacioli'nin yayımladığı İlahi Oran adlı bir çalışmasına resimler vermiştir Bu kitapta Leonardo Leonardo da Vinci tarafından yapılmış Five Platonic Solids (Beş Platonik Cisim) adlı resimler bulunmaktadır Bunlar, bir küp, bir Tetrahedron, bir Dodekahedron, bir Oktahedron ve bir Ikosahedronun resimleridir Altın Oran'ın Latince karşılığını ilk kullanan muhtemelen Leonardo da Vinci 'dir Rönesans sanatçıları Altın Oran'ı tablolarında ve heykellerinde denge ve güzelliği elde etmek amacıyla sıklıkla kullanmışlardır Örneğin Leonardo da Vinci, Son Yemek adlı tablosunda, İsa'nın ve havarilerin oturduğu masanın boyutlarından, arkadaki duvar ve pencerelere kadar Altın Oran'ı uygulamıştır Güneş etrafındaki gezegenlerin yörüngelerinin eliptik yapısını keşfeden Johannes Kepler (1571-1630), Altın Oran'ı şu şekilde belirtmiştir: "Geometrinin iki büyük hazinesi vardır; biri Pythagoras'ın teoremi, diğeri, bir doğrunun Altın Oran'a göre bölünmesidir" Bu oranı göstermek için, Parthenon'un mimarı ve bu oranı resmen kullandığı bilinen ilk kişi olan Phidias'a ithafen, 1900'lerde Yunan alfabesindeki Phi harfini Amerika'lı matematikçi Mark Barr kullanmıştır Aynı zamanda Yunan alfabesindekine karşılık gelen F harfi de, Fibonacci'nin ilk harfidir

Altın Oran, bir sayının insanlık, bilim ve sanat tarihinde oynadığı inanılmaz bir roldür Phi, evren ve yaşamı anlama konusunda bizlere yeni kapılar açmaya devam etmektedir 1970'lerde Roger Penrose, o güne kadar imkansız olduğu düşünülen, "yüzeylerin beşli simetri ile katlanması"nı Altın Oran sayesinde bulmuştur

Fibonacci Sayıları ve Altın Oran



Fibonacci sayıları (1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765 şeklinde devam eder) ile Altın Oran arasında ilginç bir ilişki vardır Dizideki ardışık iki sayının oranı, sayılar büyüdükçe Altın Oran'a yaklaşır

Fibonacci ardışıkları, Altın Oran ilişkisi yorumlamasıdır

Teoloji ve Altın Oran

Doğada, pek çok canlıda(insan da dahil) bu oran görülmektedirBazıları, bu oranın doğada bir ölçü olduğunun kanıtı olduğunu ileri sürerAltın Oran'ın Kuran'daki şu âyetle ilişkili olduğu öne sürülmüştür:

"Allah, her şey için bir ölçü kılmıştır" (Talak Suresi, 3)

Altın Oran'ı anlatmanın en iyi yollarından biri, işe bir kare ile başlamaktır





Bir kareyi tam ortasından iki eşit diktörgen oluşturacak şekilde ikiye bölelim





Dikdörtgenlerin ortak kenarının, karenin tabanını kestiği noktaya pergelimizi koyalım Pergelimizi öyle açalım ki, çizeceğimiz daire, karenin karşı köşesine değsin, yani yarı çapı, bir dikdörtgenin köşegeni olsun





Sonra, karenin tabanını, çizdiğimiz daireyle kesişene kadar uzatalım





Yeni çıkan şekli bir dikdörtgene tamamladığımızda, karenin yanında yeni bir dikdörtgen elde etmiş olacağız





İşte bu yeni dikdörtgenin taban uzunluğunun (B) karenin taban uzunluğuna (A) oranı Altın Oran'dır Karenin taban uzunluğunun (A) büyük dikdörtgenin taban uzunluğuna (C) oranı da Altın Oran'dır A / B = 16180339 = Altın Oran C / A = 16180339 = Altın Oran





Elde ettiğimiz bu dikdörtgen ise, bir Altın Dikdörtgen'dir Çünkü kısa kenarının, uzun kenarına oranı 1618 dir, yani Altın Oran'dır





Artık bu dikdörtgenden her bir kare çıkardığımızda elimizde kalan, bir Altın Dikdörtgen olacaktır






İçinden defalarca kareler çıkardığımız bu Altın Dikdörtgen'in karelerinin kenar uzunluklarını yarıçap alan bir çember parçasını her karenin içine çizersek, bir Altın Spiral elde ederiz Altın Spiral, birçok canlı ve cansız varlığın biçimini ve yapı taşını oluştururBuna örnek olarak Ayçiçeği bitkisini gösterebiliriz Ayçiçeğinin çekirdekleri altın oranı takip eden bir spiral oluşturacak şekilde dizilirler





Bu karelerin kenar uzunlukları sırasıyla Fibonacci sayılarını verir