|
|||||||
  |
|
|
Konu Araçları |
| boolean, dijital, elektronik, matematiği, sayısal |
Sayısal (Dijital) Elektronik - Boolean Matematiği |
|
|
#1 |
|
Şengül Şirin

|
Sayısal (Dijital) Elektronik - Boolean MatematiğiSayısal (Dijital) Elektronik - Boolean Matematiği BOOLEAN MATEMATİĞİ İngiliz matematikçi George Bole tarafından 1854 yılında geliştirilen BOOLEAN matematiği sayısal devrelerin tasarımında ve analizinde kullanılması 1938 yılında Claude Shanon tarafından gerçekleştirildi  BOOLEAN matematiği sayısal devrelerin çıkış ifadelerinin giriş değişkenle ri cinsinden ifade edilmesi ve elde edilen ifadenin en basit haline ulaşması için kullanılır BOOLEAN matematiği sayısal devrelerin çıkış ifadelerinin giriş değişkenle ri cinsinden ifade edilmesi ve elde edilen ifadenin en basit haline ulaşması için kullanılır Bu bölümde aşağıdaki konular anlatılacaktır Bu bölümde aşağıdaki konular anlatılacaktır DEĞİL,VE,VEYA,VEDEĞİL ve VEYADEĞİL kapılarının, BOOLEAN Matematiği ifadeleri  BOOLEAN matematiğinde temel kuralların ve kanunların uygulanması BOOLEAN matematiğinde temel kuralların ve kanunların uygulanması BOOLEAN ifadelerinde DeMorgan teoreminin uygulanması BOOLEAN ifadelerinde DeMorgan teoreminin uygulanması BOOLEAN ifadelerinden sayısal devrenin çizilmesi,bir sayısal devreden Boolean ifadesinin elde edilmesi BOOLEAN ifadelerinden sayısal devrenin çizilmesi,bir sayısal devreden Boolean ifadesinin elde edilmesi BOOLEAN ifadelerinin kanunlar ve kurallar yardımı ile sadeleştirilmesi BOOLEAN ifadelerinin kanunlar ve kurallar yardımı ile sadeleştirilmesi BOOLEAN ifadelerinin doğruluk tablolarından elde edilmesi ve BOOLEAN açılmları ve standart ifadeler BOOLEAN ifadelerinin doğruluk tablolarından elde edilmesi ve BOOLEAN açılmları ve standart ifadeler   BOOLEAN açılımların birbirlerine dönüşümü BOOLEAN açılımların birbirlerine dönüşümü  Sayısal işlemler Sayısal işlemler4  1 1 BOOLEAN İŞLEMLERİ BOOLEAN İŞLEMLERİBoolean matematiği sayısal sistemlerin analizinde ve anlaşılmasında kullanılan temel sistemdir  Bu bölümde temel Boolean işlemleri ve bunların sayısal devrelerde nasıl kullanıldığı anlatılacaktır Bu bölümde temel Boolean işlemleri ve bunların sayısal devrelerde nasıl kullanıldığı anlatılacaktır 4  1 1 1 BOOLEAN MATEMATİĞİ SEMBOLLERİ 1 BOOLEAN MATEMATİĞİ SEMBOLLERİBoolean matematiğinde kullanılan değişkenler veya fonksiyonlar büyük harfler kullanılarak gösterilmiştir  Sayısal olarak bir değişken veya fonksiyon iki değer alabilir Sayısal olarak bir değişken veya fonksiyon iki değer alabilir Bu değerler 1 veya 0 olacaktır Bu değerler 1 veya 0 olacaktır Değişkenlerin veya fonksiyonların aldığı bu değerler sayısal devrelerde eğer “1” ise YÜKSEK gerilim seviyesi , “0” ise ALÇAK gerilim seviyesini gösterecektir Değişkenlerin veya fonksiyonların aldığı bu değerler sayısal devrelerde eğer “1” ise YÜKSEK gerilim seviyesi , “0” ise ALÇAK gerilim seviyesini gösterecektir  A ve B girişlere uygulanan iki değişkeni gösterirse VE fonksiyonu Boolen ifadesi olarak ‘A  B’ şeklinde yazılırken, VEYA fonksiyonu için ‘A+B’ şeklinde yazılacaktır B’ şeklinde yazılırken, VEYA fonksiyonu için ‘A+B’ şeklinde yazılacaktır 4  1 1 2 BOOLEAN TOPLAMA VE ÇARPMA 2 BOOLEAN TOPLAMA VE ÇARPMABoolean toplamaya ilişkin temel kurallar aşağıda verilmiştir   4  2 2 BOOLEAN KANUNLARI BOOLEAN KANUNLARIBoolen matematiğinin üç temel kanunu: Yer değiştirme kanunu( Commutative Laws), Birleşme kanunu (Associative Laws) ve Dağılma Kanunu (Distributive Laws) adını alırlar  YER DEĞİŞTİRME KANUNU( COMMUTATİVE LAWS) İki giriş değişkeni için Boolean toplamaya ait yer değiştirme kanunu aşağıdaki gibi yazılır  BİRLEŞME KANUNU (ASSOCİATİVE LAWS) Boolean toplama işlemine ilişkin birleşme kanunu A,B,C giriş değişkenlerini göstermek üzere aşağıdaki gibi yazılır   DAĞILMA KANUNU (DISTRIBUTIVE LAW) A,B,C giriş değişkenlerini göstermek üzere dağılma kanunu aşağıdaki gibi yazılır  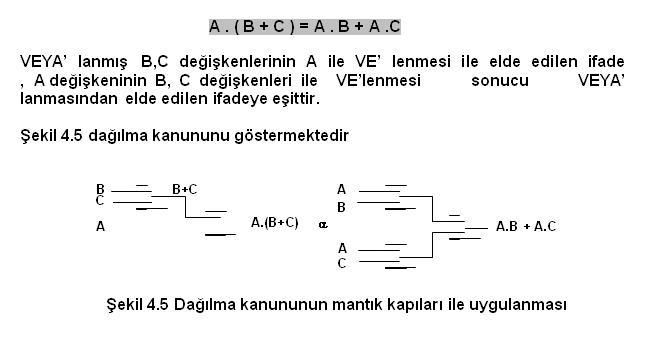 4  3 BOOLEAN MATEMATİĞİ KURALLARI 3 BOOLEAN MATEMATİĞİ KURALLARI Kural 1- VEYA özdeşlikleri a) Bir VEYA kapısının girişlerinden biri “0” ise çıkış ifadesi A’ nın durumuna bağlıdır  Eğer A=0 ise çıkış “0”, A=1 ise çıkış “1” olur Eğer A=0 ise çıkış “0”, A=1 ise çıkış “1” olur b) Bir VEYA kapısının girişlerinden biri “1” ise , A’ nın durumu ne olursa olsun çıkış daima “1” olur  c) Bir VEYA kapısının girişlerine değişkenin değili ile kendisi uygulanırsa çıkış A’nın durumu ne olursa olsun daima “1” olur  d) Bir VEYA kapısının her iki girişine aynı değişken uygulanırsa çıkış A’nın durumuna bağlıdır  Eğer A=0 ise çıkış “0”, =1 ise çıkış “1” olur   Kural 2- VE özdeşlikleri a) Bir VE kapısının girişlerinden biri “0” ise, A’ nın durumu ne olursa olsun çıkış daima “0”olur  b) Bir VE kapısının girişlerinden biri “1” ise çıkış ifadesi A’ nın durumuna bağlıdır  Eğer A=0 ise çıkış “0”, A=1 ise çıkış “1” olur Eğer A=0 ise çıkış “0”, A=1 ise çıkış “1” olur c) Bir VE kapısının girişlerine değişkenin değili(tümleyeni) ile kendisi uygulanırsa çıkış A’nın durumu ne olursa olsun daima “0” olur  d) Bir VE kapısının her iki girişine aynı değişken uygulanırsa çıkış A’nın durumuna bağlıdır  Eğer A=0 ise çıkış “0”, A=1 ise çıkış “1” olur Eğer A=0 ise çıkış “0”, A=1 ise çıkış “1” olur 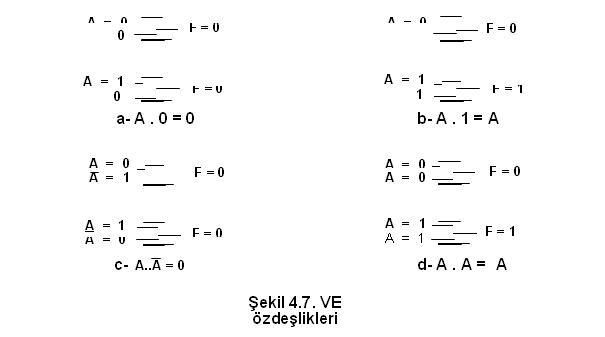 Kural 3- Çift tersleme kuralı Bir Lojik ifadenin veya değişkenin iki defa değili alınırsa (terslenirse) lojik ifadenin veya değişkenin aslı elde edilir 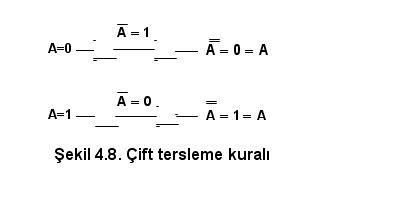 Kural 4- Yutma kuralı Bu kuralı dağılma kanunu ve VEYA, VE özdeşlikleri yardımı ile açıklayalım  Eğer ifadeyi A ortak parantezine alırsak aşağıdaki dönüşüm sağlanmış olur Eğer ifadeyi A ortak parantezine alırsak aşağıdaki dönüşüm sağlanmış olur  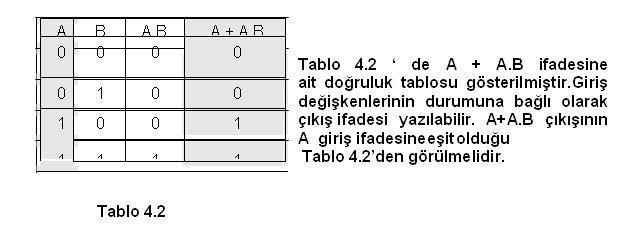 Kural 5  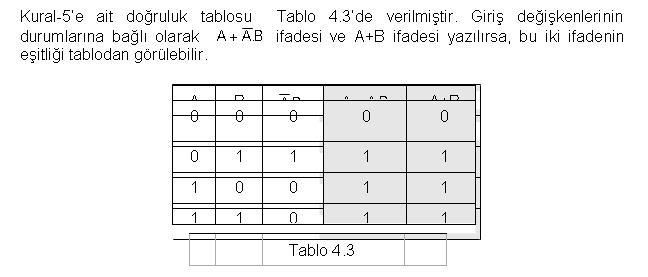 Kural 6 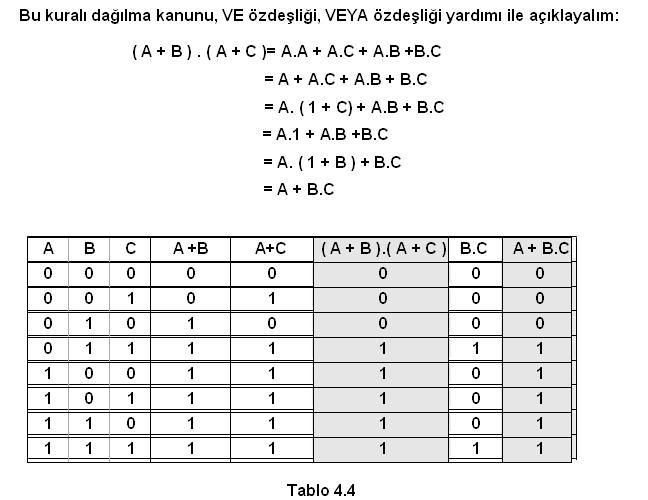 Tablo 4  4’de girişlerin durumuna bağlı olarak 4’de girişlerin durumuna bağlı olarak( A + B)  ( A + C ) ile A + B ( A + C ) ile A + B C Cifadelerinin durumları yazılmıştır  Bu iki ifadenin eşitliği tablodan görülebilir Bu iki ifadenin eşitliği tablodan görülebilir <!-- icon and title --> Boolean Matematiği <!-- / icon and title --> <!-- message --> 4  4 DEMORGAN TEOREMLERİ 4 DEMORGAN TEOREMLERİ 
__________________
Arkadaşlar, efendiler ve ey millet, iyi biliniz ki, Türkiye Cumhuriyeti şeyhler, dervişler, müritler, meczuplar memleketi olamaz
 En doğru, en hakiki tarikat, medeniyet tarikatıdır En doğru, en hakiki tarikat, medeniyet tarikatıdır |

|
Cevap : Sayısal (Dijital) Elektronik - Boolean Matematiği |
|
|
#2 |
|
Şengül Şirin

|
Cevap : Sayısal (Dijital) Elektronik - Boolean Matematiği    4  5 SAYISAL DEVRE TASARIMI 5 SAYISAL DEVRE TASARIMIBoolean ifadesinden mantık kapıları arasında uygun bağlantılar yapılması ile sayısal devrenin elde edilmesi işlemine sayısal devre tasarımı adı verilir  Bu bölümde verilen bir Boolean ifadesinden sayısal devrenin çizimi ve sayısal devrelerden Boolean ifadesinin elde edilmesi anlatılacaktır Bu bölümde verilen bir Boolean ifadesinden sayısal devrenin çizimi ve sayısal devrelerden Boolean ifadesinin elde edilmesi anlatılacaktır 4  5 5 1 BOOLEAN İFADESİNDEN SAYISAL DEVRELERİN ÇİZİLMESİ 1 BOOLEAN İFADESİNDEN SAYISAL DEVRELERİN ÇİZİLMESİBu kısımda verilen bir Boolean ifadesinden sayısal devrelerin çizilmesi anlatılacaktır  Devre tasarlanırken ilk önce Boolean ifadesinde kaç tane giriş değişken in olduğu, daha sonra bu değişkenlerin hangi Boolean işlemine uygulandığı bulunmalıdır Devre tasarlanırken ilk önce Boolean ifadesinde kaç tane giriş değişken in olduğu, daha sonra bu değişkenlerin hangi Boolean işlemine uygulandığı bulunmalıdır Çizim sırasında Boolean matematiği işlem sırası takip edilmelidir Çizim sırasında Boolean matematiği işlem sırası takip edilmelidir İşlem sırası parantez ,DEĞİL,VE, VEYA şeklindedir İşlem sırası parantez ,DEĞİL,VE, VEYA şeklindedir    4  5 5 2 SAYISAL DEVREDEN BOOLEAN İFADESİNİN ELDE EDİLMESİ 2 SAYISAL DEVREDEN BOOLEAN İFADESİNİN ELDE EDİLMESİÇizilmiş bir sayısal devreden Boolean ifadesinin elde edilebilmesi için ilk önce kapı girişlerine uygulanan değişkenler belirlenir  Her kapı çıkışına ait Boolean ifadesi yazılır Her kapı çıkışına ait Boolean ifadesi yazılır Bu işlem devredeki en son kapıya kadar sürdürülür Bu işlem devredeki en son kapıya kadar sürdürülür  4  6 BOOLEAN İFADELERİNİN SADELEŞTİRİLMESİ 6 BOOLEAN İFADELERİNİN SADELEŞTİRİLMESİÇoğu zaman sayısal bir devre için elde edilen Boolean ifadesi uzun ve karmaşık olabilir  Devreyi bu haliyle tasarlamak işlemin maliyetinin artmasını ve hata yapma olasılığını beraberinde getirmektedir Devreyi bu haliyle tasarlamak işlemin maliyetinin artmasını ve hata yapma olasılığını beraberinde getirmektedir Boolean teorem, kural ve kanunular yardımı ile ifadeler sadeleştirilerek daha az sayıda mantık kapısı ile sayısal devreler tasarlanabilir Boolean teorem, kural ve kanunular yardımı ile ifadeler sadeleştirilerek daha az sayıda mantık kapısı ile sayısal devreler tasarlanabilir   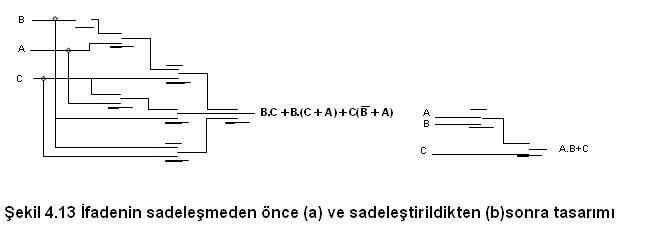 4  7 7 BOOLEAN İFADELERİNİN ELDE EDİLMESİ BOOLEAN İFADELERİNİN ELDE EDİLMESİBir doğruluk tablosu tasarımcı tarafından sayısal devrenin çalışmasına yönelik oluşturulmuş ve giriş değişkenlerinin durumuna bağlı olarak çıkışın ne olması gerektiği anlatan tablodur  Tasarım aşamasında en önemli işlemlerden biri olan doğruluk tablosunu oluşturduktan sonra ifadenin mantık kapıları ve bu k apıların birbirleriyle olan bağlantılarının elde edilebilmesi için tablodan Boolea n ifadesinin elde edilmesi gerekmektedir Tasarım aşamasında en önemli işlemlerden biri olan doğruluk tablosunu oluşturduktan sonra ifadenin mantık kapıları ve bu k apıların birbirleriyle olan bağlantılarının elde edilebilmesi için tablodan Boolea n ifadesinin elde edilmesi gerekmektedir Önceki kısımlarda bu ifadelerin sadeleştirilmesi ve devrelerin çizilmesi anlatıldı Önceki kısımlarda bu ifadelerin sadeleştirilmesi ve devrelerin çizilmesi anlatıldı Bu bölümde Boolean ifadelerinin doğruluk tablosundan elde edilmesi konusu anlatılacaktır Bu bölümde Boolean ifadelerinin doğruluk tablosundan elde edilmesi konusu anlatılacaktır 4  7 7 1 1 BOOLEAN AÇILIMLARI VE STANDART FORMLAR BOOLEAN AÇILIMLARI VE STANDART FORMLARBoolean ifadeleri fonksiyonun doğruluk tablosundan elde edilen iki temel açılımdır  Bu ifadeler eğer bir sadeleştirme işlemi uygulanmazsa az sayıda değişken içermesi ender olarak karşılaşılan bir durumdur Bu ifadeler eğer bir sadeleştirme işlemi uygulanmazsa az sayıda değişken içermesi ender olarak karşılaşılan bir durumdur Boolean ifadelerinin yazıldığı iki temel açılım minterimlerin toplamı ve maxterimlerin çarpımı olarak gösterilebilirler Boolean ifadelerinin yazıldığı iki temel açılım minterimlerin toplamı ve maxterimlerin çarpımı olarak gösterilebilirler 4  7 7 1 1 1 MİNTERİM VE MAXİTERİM 1 MİNTERİM VE MAXİTERİM 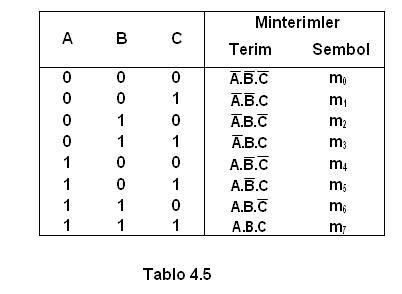 Üç değişkenin alabileceği sekiz (23) durum olduğundan 0’dan 7’ye kadar olan onluk sayıların ikilik karşılıkları, yazılabilecek durumları vermektedir  Her bir değişken ikilik sayıda eğer “0” ise değili “1” ise değişkenin kendisi yazılarak bulunur Her bir değişken ikilik sayıda eğer “0” ise değili “1” ise değişkenin kendisi yazılarak bulunur Minimum terim Boolean ifadesini “1” yapan terimdir Minimum terim Boolean ifadesini “1” yapan terimdir Her bir minimum terim mj şeklinde gösterilir Her bir minimum terim mj şeklinde gösterilir Burada j indisi ilgili ikilik sayının onluk karşılığıdır Burada j indisi ilgili ikilik sayının onluk karşılığıdır Benzer biçimde n kadar değişken için değişkenin kendisi ve değili olmak üzere VEYA işlemini ile birleştirilmiş 2n kadar durum yazılabilir  VEYA işlemi ile birleştirilmiş bu durumlar ise maksimum terimler veya standart toplama adını alırlar VEYA işlemi ile birleştirilmiş bu durumlar ise maksimum terimler veya standart toplama adını alırlar Üç değişkene ait maksimum terimler Tablo 4  6’da verilmiştir 6’da verilmiştir Her maxterim üç değişkenin VEYA işlemi ile birleştirilmiş halinden elde edilir ve burada ikilik sayıda değişken 0 ise değişkenin kendisi, 1 ise değişkenin değili yazılarak bulunabilir Her maxterim üç değişkenin VEYA işlemi ile birleştirilmiş halinden elde edilir ve burada ikilik sayıda değişken 0 ise değişkenin kendisi, 1 ise değişkenin değili yazılarak bulunabilir 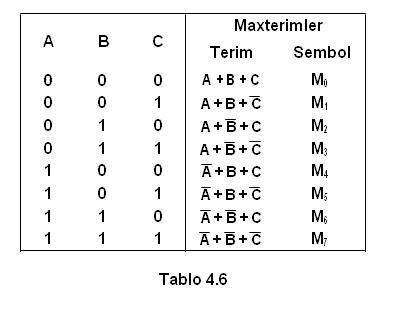
__________________
Arkadaşlar, efendiler ve ey millet, iyi biliniz ki, Türkiye Cumhuriyeti şeyhler, dervişler, müritler, meczuplar memleketi olamaz
 En doğru, en hakiki tarikat, medeniyet tarikatıdır En doğru, en hakiki tarikat, medeniyet tarikatıdır |

|
Cevap : Sayısal (Dijital) Elektronik - Boolean Matematiği |
|
|
#3 |
|
Şengül Şirin

|
Cevap : Sayısal (Dijital) Elektronik - Boolean Matematiği4  7 7 1 1 2 2 MİNİTERİMLERİN TOPLAMI Bir önceki konuda n sayıda değişkene ait 2n sayıda minimum terim yazılabileceğini MİNİTERİMLERİN TOPLAMI Bir önceki konuda n sayıda değişkene ait 2n sayıda minimum terim yazılabileceğinive bu minimum terimlerin fonksiyonu ‘1’ yapan terimler olduğu anlatılmıştı  Boolean fonksiyonunu minterimlerin toplamı (çarpımların toplamı) cinsinden ifade edebilmek için fonksiyonun ‘1’ olduğu her durum için minimum terimler bulunur Boolean fonksiyonunu minterimlerin toplamı (çarpımların toplamı) cinsinden ifade edebilmek için fonksiyonun ‘1’ olduğu her durum için minimum terimler bulunur Bulunan bu minimum terimler VEYA’lanarak fonksiyon minterimlerin toplamı(çarpımların toplamı) cinsinden yazılabilir Bulunan bu minimum terimler VEYA’lanarak fonksiyon minterimlerin toplamı(çarpımların toplamı) cinsinden yazılabilir       <!-- / message --> 4  7 7 1 1 3 3 MAXİTERİMLERİN ÇARPIMI MAXİTERİMLERİN ÇARPIMI   Şeklinde fonksiyon verilebilir  ∏ sembolü parantez içindeki maxiterimlere VE işleminin uygulanacağını gösterirken, çıkış ifadesini (Q) takip eden parantez değişkenleri (A,B,C) göstermektedir ∏ sembolü parantez içindeki maxiterimlere VE işleminin uygulanacağını gösterirken, çıkış ifadesini (Q) takip eden parantez değişkenleri (A,B,C) göstermektedir Boolean fonksiyonların maxterimlerin çarpımı (toplamların çarpımı) olarak ifade edebilmek için fonksiyonu VEYA terimleri haline getirmek gerekir  Bu işlem: Bu işlem:(A+B)  (A+C) = A+B (A+C) = A+B C Cdağılma kanunu kullanılarak gerçekleştirilir  Daha sonra her bir VEYA teriminde eksik değişken varsa , A eksik değişkeni göstermek üzere terim, Daha sonra her bir VEYA teriminde eksik değişken varsa , A eksik değişkeni göstermek üzere terim,    4  7 7 1 1 4 BOOLEAN AÇILIMLARININ BİRBİRLERİNE DÖNÜŞTÜRÜLMESİ 4 BOOLEAN AÇILIMLARININ BİRBİRLERİNE DÖNÜŞTÜRÜLMESİİki temel Boolean açılımda kullanılan minterim ve maxterimler ifade ediliş bakımından birbirlerinin tümleyeni olduğu görülebilir  Bunun nedeni fonksiyonu ‘1’ yapan terimlere ait minimum terimler bulunurken, fonksiyonu ‘0’ yapan minimum terimlerin tümleyeninin fonksiyonu ‘1’ yapmasıdır Bunun nedeni fonksiyonu ‘1’ yapan terimlere ait minimum terimler bulunurken, fonksiyonu ‘0’ yapan minimum terimlerin tümleyeninin fonksiyonu ‘1’ yapmasıdır Örneğin : Örneğin : Boolean açılımlarının birbirleri arasındaki dönüşümde; I - Dönüşüm işlemine göre a) Eğer minterimden maxterime dönüşüm isteniyorsa ∑ sembolü ile ∏ sembolü ile değiştirilir  b) Eğer maxterimden minterime dönüşüm isteniyorsa ∏ sembolü ile ∑ sembolü ile değiştirilir  II - Fonksiyonda sayılar seklinde verilen terimlerin yerlerine fonksiyonda bulunmayan sayıları yazılır  adımları takip edilebilir  Örnek : Aşağıda minterimler cinsinden verilen fonksiyonu maxterimler cinsinden yazınız  Q(x,y,z,w)=∏(0,2,3,7,9,11,12,13,15) Çözüm: Dönüşüm işlemi maxterimden minterime olduğuna göre ∏sembolü ∑ sembolü ile yer değişecektir  Fonksiyonda olmayan sayılar yazılarak dönüşüm işlemi tamamlanmış olur Fonksiyonda olmayan sayılar yazılarak dönüşüm işlemi tamamlanmış olur Q(x,y,z,w)= ∑ (1,4,5,6,8,10,14) 4  7 7 1 1 5 5 STANDART İFADELER STANDART İFADELERBoolean fonksiyonların elde etmenin bir diğer yolu standart formlardır  Bu formda fonksiyonu oluşturan terimler değişkenlerin tamamı içermetebilir Bu formda fonksiyonu oluşturan terimler değişkenlerin tamamı içermetebilir İki temel tip standart form vardır, çarpımların toplamı (Sum of Product-SOP) ve toplamların çarpımı (Product of Sum-POS) İki temel tip standart form vardır, çarpımların toplamı (Sum of Product-SOP) ve toplamların çarpımı (Product of Sum-POS) Çarpımların toplamı formu, bir veya daha fazla değişkenden oluşan çarpım terimleri olarak adlandırılan VE terimlerinden oluşmuş Boolean ifadesi gösterimidir  Toplam, elde edilen VE terimlerinin VEYA ’landığını göstermektedir Toplam, elde edilen VE terimlerinin VEYA ’landığını göstermektedir Bu forma bir örnek aşağıda gösterilmiştir Bu forma bir örnek aşağıda gösterilmiştir  4  7 7 2 DİĞER SAYISAL İŞLEMLER 2 DİĞER SAYISAL İŞLEMLERn kadar değişkene sahip bir Boolean fonksiyonu için 2n olası durum yazılabildiği için,2n n kadar değişken için yazılabilecek fonksiyon sayısı n=2 olduğundan yazılabilecek fonksiyon sayısı 16’dır  2 kadardır  İki değişken için X ve y gibi iki değişkene ait yazılabilecek 16 fonksiyona ait doğruluk tabloları Tablo 4 İki değişken için X ve y gibi iki değişkene ait yazılabilecek 16 fonksiyona ait doğruluk tabloları Tablo 4 7’de verilmiştir 7’de verilmiştir Tabloda F0’dan F15’e kadar olan 16 sütündan her birisi x ve y değişkenlerinden oluşan fonksiyonlardan birinin doğruluk tablosunu gösterm ektedir Tabloda F0’dan F15’e kadar olan 16 sütündan her birisi x ve y değişkenlerinden oluşan fonksiyonlardan birinin doğruluk tablosunu gösterm ektedir Fonksiyonlar F’in alabileceği 16 durumdan elde edilmiştir Fonksiyonlar F’in alabileceği 16 durumdan elde edilmiştir Fonksiyonların bazılarında işlemci sembolü vardır Fonksiyonların bazılarında işlemci sembolü vardır Örmeğin F1, Ve işlemine ilişkin doğruluk tablosunu vermektedir ve işlem sembolü “ Örmeğin F1, Ve işlemine ilişkin doğruluk tablosunu vermektedir ve işlem sembolü “ ” olarak verilmiştir ” olarak verilmiştir  Tablo 4  8 doğruluk tablosu verilen 16 fonksiyona ait Boolean ifadelerini göstermektedir 8 doğruluk tablosu verilen 16 fonksiyona ait Boolean ifadelerini göstermektedir Boolean ifadeleri en az sayıda değişken içerecek biçimde sadeleştirilmiştir Boolean ifadeleri en az sayıda değişken içerecek biçimde sadeleştirilmiştir Tabloda görülen fonksiyonların bir bölümü (VE,VEYA,DEĞİL vb Tabloda görülen fonksiyonların bir bölümü (VE,VEYA,DEĞİL vb ) Boolean işlemcileri ile ifade edilebilmelerine rağmen diğer fonksiyonları n ( Özel VEYA, x değil ve y vb ) Boolean işlemcileri ile ifade edilebilmelerine rağmen diğer fonksiyonları n ( Özel VEYA, x değil ve y vb ) ifade edilebilmeleri için özel işlem sembolü kullanılmıştır ) ifade edilebilmeleri için özel işlem sembolü kullanılmıştır Özel-Veya işlemi dışındaki işlem sembolleri tasarımcılar tarafından pek kullanılmaz Özel-Veya işlemi dışındaki işlem sembolleri tasarımcılar tarafından pek kullanılmaz Tablo 4  8’da verilen 16 fonksiyon üç ana gurupta incelenebilir: 8’da verilen 16 fonksiyon üç ana gurupta incelenebilir:I  İki fonksiyon ‘0’ veya ‘1’ gibi bir sabit üretir İki fonksiyon ‘0’ veya ‘1’ gibi bir sabit üretir II  Dört fonksiyon tümleyen ve transfer işlemini verir Dört fonksiyon tümleyen ve transfer işlemini verir III  On fonksiyon VE,VEYA,VEDEĞİL,VEYADEĞİL,Özel-VEYA, Özel-VEYA DEĞİL, engelleme ve içerme olmak üzere sekiz işlemi gösterir On fonksiyon VE,VEYA,VEDEĞİL,VEYADEĞİL,Özel-VEYA, Özel-VEYA DEĞİL, engelleme ve içerme olmak üzere sekiz işlemi gösterir 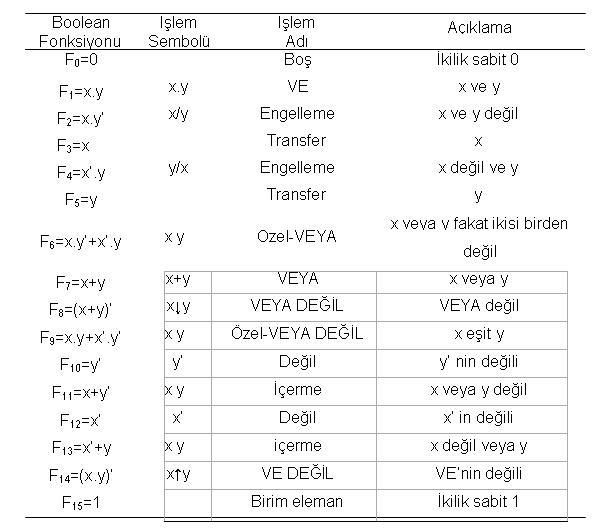 İkilik bir fonksiyon sadece ‘1’ veya ‘0’ değerlerini alabilir  Tümleyen fonksiyonu ikilik değişkenlerden (x ,y) her birisinin tümleyenini(x’,y’) verir Tümleyen fonksiyonu ikilik değişkenlerden (x ,y) her birisinin tümleyenini(x’,y’) verir Girişin değişkenlerinden birine eşit olan fonksiyona transfer fonksiyonu denir Girişin değişkenlerinden birine eşit olan fonksiyona transfer fonksiyonu denir Engeleme ve içerme işlemleri sayısal tasarımcılar tarafından kullanılsada bilgisayar mantığında nadiren kullanılr Engeleme ve içerme işlemleri sayısal tasarımcılar tarafından kullanılsada bilgisayar mantığında nadiren kullanılr VE,VEYA,VE değil,VEYA değil,Özel-VEYA ve Özel-VEYA değil işlemleri sayısal sistemlerin tasarımında yaygın olarak kullanılmaktadır VE,VEYA,VE değil,VEYA değil,Özel-VEYA ve Özel-VEYA değil işlemleri sayısal sistemlerin tasarımında yaygın olarak kullanılmaktadır
__________________
Arkadaşlar, efendiler ve ey millet, iyi biliniz ki, Türkiye Cumhuriyeti şeyhler, dervişler, müritler, meczuplar memleketi olamaz
 En doğru, en hakiki tarikat, medeniyet tarikatıdır En doğru, en hakiki tarikat, medeniyet tarikatıdır |

|
Üye olmanıza kesinlikle gerek yok !
Konuya yorum yazmak için sadece buraya tıklayınız.
Bu sitede 1 günde 10.000 kişiye sesinizi duyurma fırsatınız var.
IP adresleri kayıt altında tutulmaktadır. Aşağılama, hakaret, küfür vb. kötü içerikli mesaj yazan şahıslar IP adreslerinden tespit edilerek haklarında suç duyurusunda bulunulabilir.
Konuya yorum yazmak için sadece buraya tıklayınız.
Bu sitede 1 günde 10.000 kişiye sesinizi duyurma fırsatınız var.
IP adresleri kayıt altında tutulmaktadır. Aşağılama, hakaret, küfür vb. kötü içerikli mesaj yazan şahıslar IP adreslerinden tespit edilerek haklarında suç duyurusunda bulunulabilir.
«
Önceki Konu
|
Sonraki Konu
»
|
|
ForumSinsi.com hakkında yapılacak tüm şikayetlerde ilgili adresimizle iletişime geçilmesi halinde kanunlar ve yönetmelikler çerçevesinde en geç 1 (Bir) Hafta içerisinde gereken işlemler yapılacaktır. İletişime geçmek için buraya tıklayınız.



