|
|||||||
  |
|
|
Konu Araçları |
| dijital, elektronik, sayı, sayısal, sistemleri |
Sayısal (Dijital) Elektronik - Sayı Sistemleri |
|
|
#1 |
|
Şengül Şirin

|
Sayısal (Dijital) Elektronik - Sayı SistemleriSayısal (Dijital) Elektronik - Sayı Sistemleri 1  1 1 SAYISAL (DİJİTAL) ELEKTRONİK SAYISAL (DİJİTAL) ELEKTRONİKGünümüz Elektroniği Analog ve Sayısal olmak üzere iki temel türde incelenebilir  Analog büyüklükler sonsuz sayıda değeri içermesine rağmen Sayısal büyüklükler sadece iki değer alabilirler Analog büyüklükler sonsuz sayıda değeri içermesine rağmen Sayısal büyüklükler sadece iki değer alabilirler Analog büyüklüklere örnek olarak Basınç,Sıcaklık gibi bir çok fiziksel büyüklüğü örnek olarak verebiliriz Analog büyüklüklere örnek olarak Basınç,Sıcaklık gibi bir çok fiziksel büyüklüğü örnek olarak verebiliriz Şekil1 Şekil1 1’ deki Elektrik devresinde çıkış gerilimi ayarlı direncin değiştirilmesi ile birlikte 0 ile 12 Volt arasında sonsuz sayıda değer alabilir 1’ deki Elektrik devresinde çıkış gerilimi ayarlı direncin değiştirilmesi ile birlikte 0 ile 12 Volt arasında sonsuz sayıda değer alabilir Şekil 2 Şekil 2 2’deki devrenin çıkış gerilimi sadece iki gerilim seviyesinde tanımlanabilir 2’deki devrenin çıkış gerilimi sadece iki gerilim seviyesinde tanımlanabilir Eğer anahtar açıksa 0 Volt, anahtar kapalı ise 12 Volt devrenin çıkış geriliminin alabileceği değerlerdir Eğer anahtar açıksa 0 Volt, anahtar kapalı ise 12 Volt devrenin çıkış geriliminin alabileceği değerlerdir 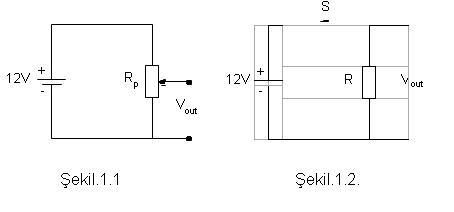 Sayısal bir sistemde bilgiler sinyal adı verilen fiziksel niceliklerle temsil edilir  Sayısal Sistemlerin çoğu sadece iki değeri olan sinyallerle çalışıyorsa bir hesap makinesinin sadece iki voltaj seviyesini kullanarak nasıl 1974 gibi bir sayıyı nasıl tanımlayabilmektedir Sayısal Sistemlerin çoğu sadece iki değeri olan sinyallerle çalışıyorsa bir hesap makinesinin sadece iki voltaj seviyesini kullanarak nasıl 1974 gibi bir sayıyı nasıl tanımlayabilmektedir Böyle bir sorunun cevabı ise Sayısal Sistemlerin normal hayatta kullandığımız Decimal (Onluk) sayı sistemini değil Binary (İkilik) tabanda kodlanmış sayı sistemini kullandığıdır Böyle bir sorunun cevabı ise Sayısal Sistemlerin normal hayatta kullandığımız Decimal (Onluk) sayı sistemini değil Binary (İkilik) tabanda kodlanmış sayı sistemini kullandığıdır 1  2 2 SAYISAL MANTIK SEVİYELERİ VE DALGA FORMLARI SAYISAL MANTIK SEVİYELERİ VE DALGA FORMLARIBir Sayısal Sistem iki gerilim seviyesine göre çalışır  Bu nedenle her Sayısal Bu nedenle her SayısalSistemin bu iki gerilim seviyesine karşılık gelen bir biçimi olmalıdır  Bu nedenle Sayısal Devreler Binary (İkilik) Sayı sisteminde kullanılan 1 ve 0 ile tanımlanmak zorundadır Bu nedenle Sayısal Devreler Binary (İkilik) Sayı sisteminde kullanılan 1 ve 0 ile tanımlanmak zorundadır Bu Sayısal Sistemin girdilerinin ikilik koda dönüşmesini sağlar Bu Sayısal Sistemin girdilerinin ikilik koda dönüşmesini sağlar Aşağıdaki Pozitif Mantık ifadelerini kullanarak Sayısal kavramları tanımlayabileceğiz  Örneğin bir anahtarın kapalı olması sayısal sistemde ‘1’ veya 5V’a eşit olacaktır Örneğin bir anahtarın kapalı olması sayısal sistemde ‘1’ veya 5V’a eşit olacaktır 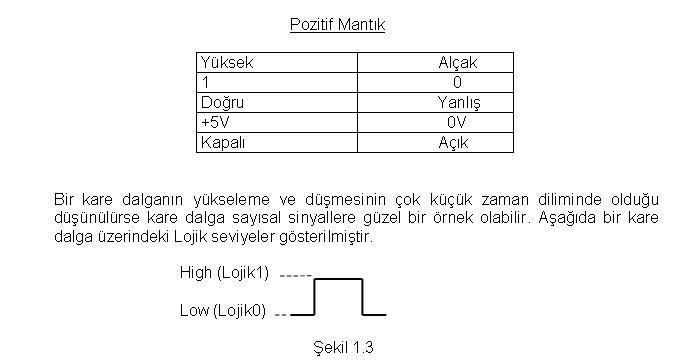 Sayısal devrelerde negatif mantık kullanımı bazı uygulamalarda tasarımcıya büyük kolaylıklar sağlamaktadır  Örneğin elektriksel gürültü problemi yaşanan sistemlerin tasarımında Negatif mantık kullanımı gürültü probleminin ortadan kalkmasını sağlayabilir Örneğin elektriksel gürültü problemi yaşanan sistemlerin tasarımında Negatif mantık kullanımı gürültü probleminin ortadan kalkmasını sağlayabilir 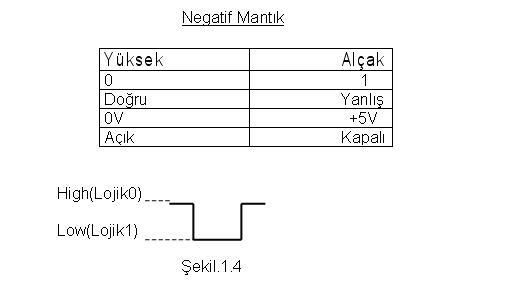 2  1 1 DECİMAL(ONLU) SAYI SİSTEMİ Decimal(Onlu) Sayı sistemi günlük hayatta kullandığımız 0,1,2,3,4,5,6,7,8,9 rakamlarından oluşur DECİMAL(ONLU) SAYI SİSTEMİ Decimal(Onlu) Sayı sistemi günlük hayatta kullandığımız 0,1,2,3,4,5,6,7,8,9 rakamlarından oluşur Decimal(Onlu) Sayı sisteminde her sayı bulunduğu basamağa göre değer alır Decimal(Onlu) Sayı sisteminde her sayı bulunduğu basamağa göre değer alır Sistemin tabanı 10’dur Sistemin tabanı 10’dur Örneğin 128 sayısı ; 128=1x10² + 2x10¹ + 8x10º 128=1x100 + 2x10 + 8x1 128=100 + 20 + 8 şeklinde yazılacaktır  Örnekten görüldüğü gibi Decimal(Onlu) bir sayıda her basamak farklı üstel ifadelerle gösterilmiştir Örnekten görüldüğü gibi Decimal(Onlu) bir sayıda her basamak farklı üstel ifadelerle gösterilmiştir Bu üstel ifade o basamağın ağırlığı olarak adlandırılır Bu üstel ifade o basamağın ağırlığı olarak adlandırılır O halde Decimal(Onlu) bir sayıyı analiz ederken basamaklardaki rakam ile basamak ağırlığını çarpmamız gerekiyor O halde Decimal(Onlu) bir sayıyı analiz ederken basamaklardaki rakam ile basamak ağırlığını çarpmamız gerekiyor Örnekte 3 Örnekte 3 basamaktaki 1sayısı 100 ile, 2 basamaktaki 1sayısı 100 ile, 2 basamaktaki 2 sayısı 10 ile ve 1 basamaktaki 2 sayısı 10 ile ve 1 Basamaktaki 8 sayısı 1 ile çarpılır Basamaktaki 8 sayısı 1 ile çarpılır Her basamaktaki çarpım sonucu toplanarak analiz sonlandırılır Her basamaktaki çarpım sonucu toplanarak analiz sonlandırılır  Örnek: Decimal(Onlu) 2784 sayısının analizini yapalım; 2784= 2x10³+7x10²+8x10¹+4x10º 2784=2x1000+3x100+8x10+4x1 2784=2000+700+80+4 2784=2784 şeklinde tanımlayabiliriz  2  1 1 1 1 ONDALIKLI DECİMAL(ONLU) SAYILAR Eğer verilen Decimal(Onlu) sayı ondalıklı ise bu durumda normal analiz işlemi devam eder yalnız ondalıklı ifadeyi 0’ı takip eden negatif sayılarla tanımlarız ONDALIKLI DECİMAL(ONLU) SAYILAR Eğer verilen Decimal(Onlu) sayı ondalıklı ise bu durumda normal analiz işlemi devam eder yalnız ondalıklı ifadeyi 0’ı takip eden negatif sayılarla tanımlarız Örnek: 568,25 sayısının analizini yapınız  568,25=5x10²+6x10¹+8x10º+2x10-¹ +5x10-² 568,25=500+60+8+0,2+0,05 568,25=568,25 şeklinde tamamlanabilir 
__________________
Arkadaşlar, efendiler ve ey millet, iyi biliniz ki, Türkiye Cumhuriyeti şeyhler, dervişler, müritler, meczuplar memleketi olamaz
 En doğru, en hakiki tarikat, medeniyet tarikatıdır En doğru, en hakiki tarikat, medeniyet tarikatıdır |

|
Cevap : Sayısal (Dijital) Elektronik - Sayı Sistemleri |
|
|
#2 |
|
Şengül Şirin

|
Cevap : Sayısal (Dijital) Elektronik - Sayı Sistemleri2  2 2 BİNARY (İKİLİK) SAYI SİSTEMİ Binary (İkilik) Sayı sisteminin tabanı 2’dir BİNARY (İKİLİK) SAYI SİSTEMİ Binary (İkilik) Sayı sisteminin tabanı 2’dir Ve bu sistemde sadece “0” ve “1” rakamları kullanılmaktadır Ve bu sistemde sadece “0” ve “1” rakamları kullanılmaktadır Binary Sayı sisteminde’ de Decimal(Onlu) Sayı sisteminde olduğu gibi her sayı bulunduğu basamağın konum ağırlığı ile çarpılır Binary Sayı sisteminde’ de Decimal(Onlu) Sayı sisteminde olduğu gibi her sayı bulunduğu basamağın konum ağırlığı ile çarpılır Binary(İkilik) Sayı Sisteminde bulunan her ‘0’ veya ‘1’ rakamları BİT (BInary DigiT) adı ile tanımlanır  Binary(İkili) sayılar yazılırken en sağdaki basamağa en düşük değerlikli bit (Least Significant Bit-LSB),en soldaki basamağa en yüksek değerlikli bit Binary(İkili) sayılar yazılırken en sağdaki basamağa en düşük değerlikli bit (Least Significant Bit-LSB),en soldaki basamağa en yüksek değerlikli bit(Most Significant Bit-MSB) adı verilir  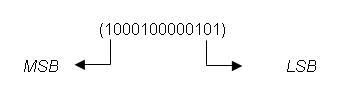 Decimal(Onlu) Sayılıları sadece iki rakamdan oluşan Binary(İkilik) sayılarla tanımlayabilmemiz Sayısal Sistemlerin iki voltaj seviyesini kullanarak farklı büyüklükleri tanımlanmasının anlaşılmasını sağlamaktadır  2  2 2 1 1 BİNARY SAYILARIN YAZILIŞI VE DECİMAL SAYILARA ÇEVRİLMESİ BİNARY SAYILARIN YAZILIŞI VE DECİMAL SAYILARA ÇEVRİLMESİBinary sayıların yazımında tabanın iki olduğu unutulmamalıdır  Binary(ikili) sayıları Decimal(Onlu) sayılara dönüştürürken her bir bit basamak ağırlığı ile çarpılıp bu sonuçların toplanması gerekir Binary(ikili) sayıları Decimal(Onlu) sayılara dönüştürürken her bir bit basamak ağırlığı ile çarpılıp bu sonuçların toplanması gerekir  Birkaç örnekle hem Binary sayıların yazımını ve Decimal(Onlu) sayılara dönüşümünü inceleyelim  Örnek: (1010)2 = ( ? )10 (1010)2 = 1 x 23 + 0 x 22 + 1 x 21 + 0 x 20 (1010)2 = 8 + 0 + 2 + 0 (1010)2 = 10 Örnek: (11001)2 = ( ? )10 (11001)2 = 1x 24+1x 23+0x 22+0x 21+1x 20 (11001)2 = 16 + 8 + 0 + 0 + 1 (11001)2 = 25 Not: Binary (İkilik) sayıların Decimal(Onlu) karşılıkları bulunurken her basamak kendi basamak ağırlığı ile çarpılır  Çarpım sonuçları toplanarak dönüşüm tamamlanır Çarpım sonuçları toplanarak dönüşüm tamamlanır Örnek: Aşağıda verilen Binary(İkilik) sayıların Decimal(Onlu) (Onlu ) karşılıklarını bulunuz  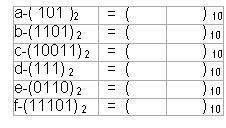 2  2 2 2 2 ONDALIKLI BİNARY SAYILARIN DECİMAL SAYILARA DÖNÜŞTÜRÜLMESİ ONDALIKLI BİNARY SAYILARIN DECİMAL SAYILARA DÖNÜŞTÜRÜLMESİOndalıklı Binary (ikilik) sayıları Decimal (onlu) sayılara dönüştürmek için izlenilecek yol çarpım iki metodudur  Ondalıklı kısma kadar olan kısmı normal analiz yöntemini kullanarak dönüştürürken ondalıklı kısmın basamak ağırlığı 0’ı takip eden negatif Ondalıklı kısma kadar olan kısmı normal analiz yöntemini kullanarak dönüştürürken ondalıklı kısmın basamak ağırlığı 0’ı takip eden negatifsayılar olarak belirlenir  Örnek: ( 111,101 )2 = (?)10 ( 111,101 )2 = 1x2²+1x2¹+1x2º+1x2¯¹+0x2¯²+1x2¯³ ( 111,101 )2 = 1x4+1x2+1x1+1x½+0x¼+1x⅛ ( 111,101 )2 = 4+2+1+0,5+0+0,125 ( 111,101 )2 = (7,625)10 Örnek: Aşağıda verilen Ondalıklı Binary (İkilik) sayıların Decimal(Onlu) karşılıklarını bulunuz  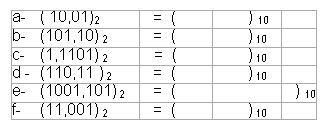 2  2 2 3 3 DECİMAL SAYILARIN BİNARY SAYILARA ÇEVRİLMESİ DECİMAL SAYILARIN BİNARY SAYILARA ÇEVRİLMESİDecimal(Onlu) sayıları Binary(İkilik) sayılara çevirirken “Bölme-2” metodu kullanılır  Çıkan sonuç tersinden yazılır Çıkan sonuç tersinden yazılır 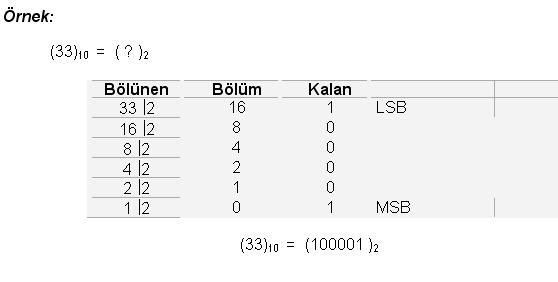 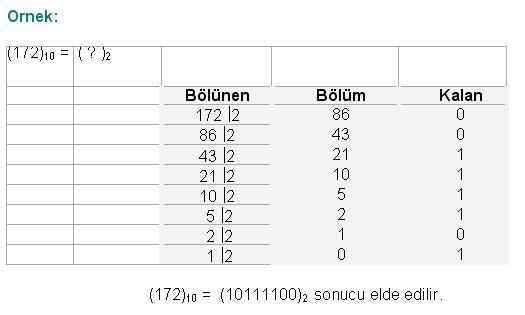 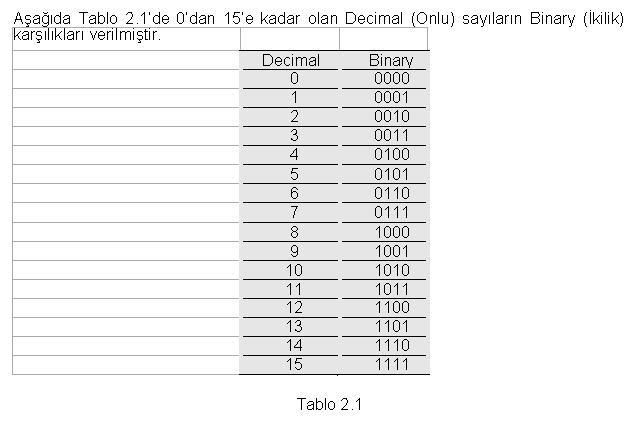 İkili sayı sistemi, sayısal sistemlerin bilgiyi tanımlayabilmesi için yeterli olmasına rağmen fazla sayıda basamak kullanılması, bu sayı sistemi ile ilgili işlemlerin çok uzun sürmesi hata olasılığını beraberinde getirmektedir  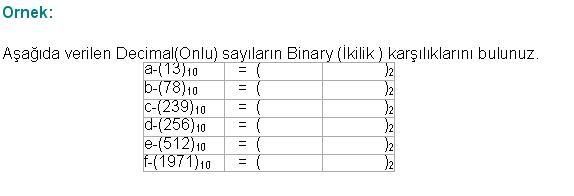 2  2 2 4 4 ONDALIKLI DECİMAL SAYILARIN BİNARY SAYILARA ONDALIKLI DECİMAL SAYILARIN BİNARY SAYILARADÖNÜŞTÜRÜLMESİ Ondalıklı Decimal(Onlu) Sayıların Binary(İkilik) karşılıkları bulunurken ondalıklı kısma kadar olan bölüm için normal çevirim yöntemi uygulanır  Ondalıklı kısım, kesirli kısmın sıfıra veya sıfıra yakın bir değere ulaşıncaya kadar 2 ile çarpılır Ondalıklı kısım, kesirli kısmın sıfıra veya sıfıra yakın bir değere ulaşıncaya kadar 2 ile çarpılır Örnek: (7,8125)10 = ( ? )2 ondalıklı decimal(onluk) sayısının binary(ikilik) karşılığını yazınız  Örnek: Aşağıdaki Ondalıklı Decimal sayıları Binary Sayılara dönüştürün; a-(0,125)10 = ( ? )2 b-(11,1451)10 = ( ? )2 c-(125,65)10 = ( ? )2 2  2 2 5 5 BİNARY SAYI SİSTEMİ ARİTMETİĞİ BİNARY SAYI SİSTEMİ ARİTMETİĞİ2  2 2 5 5 1 1 BİNARY SAYILARDA TOPLAMA BİNARY SAYILARDA TOPLAMA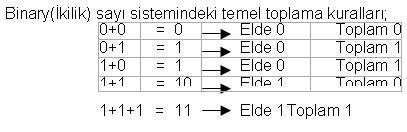 şeklinde belirtilebilir  Binary sayı sisteminde de iki sayı toplandığında eğer sonuç bir haneye sığmıyorsa bir elde(cary) oluşur Binary sayı sisteminde de iki sayı toplandığında eğer sonuç bir haneye sığmıyorsa bir elde(cary) oluşur  En sağdaki sütun 1 + 1 = 0 1 oluşan elde bir üst basamakla toplanır Ortadaki sütün 1 + 1 + 0 = 0 1 oluşan elde bir üst basamakla toplanır En soldaki sütun 1 +0 + 0 = 1 0 Not: Eğer en yüksek değerlikli basamakların toplamında bir elde oluşmuş olsaydı, bu toplam sonucunun en yüksek değerlikli biti olarak karşımıza çıkardı  
__________________
Arkadaşlar, efendiler ve ey millet, iyi biliniz ki, Türkiye Cumhuriyeti şeyhler, dervişler, müritler, meczuplar memleketi olamaz
 En doğru, en hakiki tarikat, medeniyet tarikatıdır En doğru, en hakiki tarikat, medeniyet tarikatıdır |

|
Cevap : Sayısal (Dijital) Elektronik - Sayı Sistemleri |
|
|
#3 |
|
Şengül Şirin

|
Cevap : Sayısal (Dijital) Elektronik - Sayı SistemleriNot: Eğer en yüksek değerlikli basamakların toplamında bir elde oluşmuş olsaydı, bu toplam sonucunun en yüksek değerlikli biti olarak karşımıza çıkardı   2  2 2 5 5 2 BİNARY SAYILARDA ÇIKARMA 2 BİNARY SAYILARDA ÇIKARMA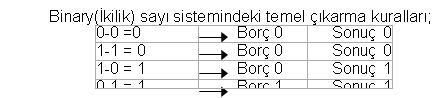 şeklinde belirtilebilir  Binary sayı sisteminde de küçük değerlikli bir basamaktan büyük Binary sayı sisteminde de küçük değerlikli bir basamaktan büyükdeğerlikli bir basamak çıkarıldığında,bir üstteki basamaktan bir borç(borrov) alınır ve çıkarma işlemi tamamlanır  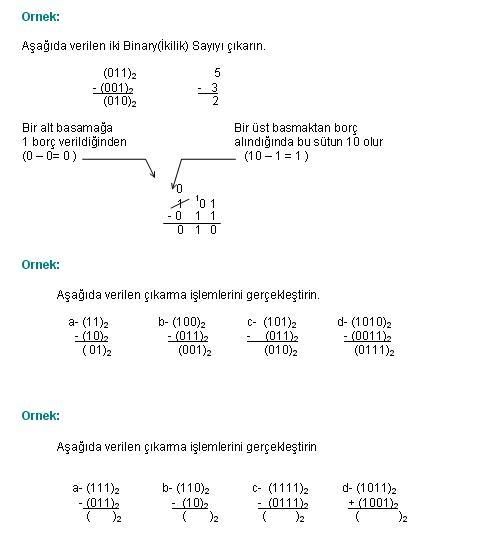 2  2 2 5 5 2 2 1TAMAMLAYICI (KOMPLEMENTER) ARİTMETİĞİ 1TAMAMLAYICI (KOMPLEMENTER) ARİTMETİĞİSayı sistemlerinde direkt çıkarma yapılacağı gibi Tamamlayıcı (Komplementer) yöntemiyle de çıkarma yapılabilir Tamamlayıcı (Komplementer) yöntemiyle çıkarma işlemi aslında bir toplama işlemidir  Bu işlemde bir üst basamaktan borç alınmaz Bu işlemde bir üst basamaktan borç alınmaz Her sayı sistemine ilişkin iki adet tümleyen (komplementer) bulunabilir Her sayı sistemine ilişkin iki adet tümleyen (komplementer) bulunabilir Bunlar; r sayı sisteminin tabanını göstermek üzere Bunlar; r sayı sisteminin tabanını göstermek üzere1  r-1 r-1 Komplementer Komplementer2  r r Komplementer Komplementerolarak gösterilebilir  Taban yerine konduğunda bu iki tümleyen (komplementer) Binary(İkilik) sayılarda 1 Taban yerine konduğunda bu iki tümleyen (komplementer) Binary(İkilik) sayılarda 1 ve 2 ve 2 Tümleyen (komplementer), Decimal(Onlu) sayılarda Tümleyen (komplementer), Decimal(Onlu) sayılarda9  ve 10 ve 10 Tümleyen (komplementer) adını alır Tümleyen (komplementer) adını alır r-1 Tümleyen (komplementer) n haneli bir tamsayı kısmı ve m haneli bir kesiri bulunan r tabanında bir N pozitif sayı için: r-1  Komplementeri = rn-r-m-N Komplementeri = rn-r-m-Nolur  r  Tümleyen (komplementer) Tümleyen (komplementer)n haneli bir tamsayı kısmı bulunan r tabanında bir N pozitif sayı için , N’ in r  Komplementeri = rn- N şeklinde bulunur Komplementeri = rn- N şeklinde bulunur Not: Binary sayılarda kolay bir yöntem olarak 2’ ye tümleyen 1’e tümleyene “1” eklenerek elde edilebilir  2’ye tümleyen = 1’ e tümleyen+1 Bire-Tümleyenle Çıkarma: Bir Binary(ikilik) sayının 1  Komplementeri basitçe her bir bitin tersinin Komplementeri basitçe her bir bitin tersininalınması ile bulunur  İki Binary(İkilik) sayıyı 1 İki Binary(İkilik) sayıyı 1 Tümleyen (komplementer) yardımı ile çıkarmak için; Tümleyen (komplementer) yardımı ile çıkarmak için;a) Çıkan sayının 1  Tümleyen (komplementer)i bulunur Tümleyen (komplementer)i bulunur 1 1 Tümleyen Tümleyen(komplementer) bulunurken çıkan sayı ile çıkarılan sayının basamak sayısının eşit olması gerekir  b) Çıkarılan sayı ile çıkan sayının 1  Tümleyen (komplementer)i toplanır Tümleyen (komplementer)i toplanır c) En büyük değerlikli basamakta elde 1 oluşursa bu işlem sonucunun pozitif olduğu anlamına gelir d) Doğru sonuca ulaşmak için elde 1 buradan alınarak en küçük değerlikli basamakla toplanır  e) Eğer elde 1 oluşmamışsa sonuç negatiftir doğru cevabı bulmak için sonuç terslenerek yazılır    İkiye-Tümleyenle Çıkarma: Binary sayının 2  Tümleyen (komplementer)i o sayının 1 Tümleyen (komplementer)i o sayının 1 Tümleyene (komplementer) Tümleyene (komplementer)1 eklenerek bulunur  2  Tümleyen (komplementer)= 1 Tümleyen (komplementer)= 1 Tümleyen (komplementer)+1 Tümleyen (komplementer)+1İki Binary sayıyı 2  Tümleyen (komplementer) yardımı ile birbirinden çıkarmak için; Tümleyen (komplementer) yardımı ile birbirinden çıkarmak için;a) Çıkan sayının 2  Tümleyen (komplementer)i bulunur Tümleyen (komplementer)i bulunur Çıkan sayı ile çıkarılan sayının basamak sayıları eşit olmalıdır Çıkan sayı ile çıkarılan sayının basamak sayıları eşit olmalıdır b) Çıkarılan sayı ile çıkan sayının 2  tümleyen (komplementer)i toplanır tümleyen (komplementer)i toplanır c) Eğer toplama işlemi sonucunda en yüksek değerlikli basamakta bir elde oluşmuşsa çıkan sonuç pozitiftir, elde atılarak gerçek sonuca ulaşılır  d) Toplam sonucunda bir elde oluşmamışsa sonuç negatiftir  Çıkan sonucun tersi alındıktan sonra 1 eklenerek gerçek sonuca ulaşılır Çıkan sonucun tersi alındıktan sonra 1 eklenerek gerçek sonuca ulaşılır  
__________________
Arkadaşlar, efendiler ve ey millet, iyi biliniz ki, Türkiye Cumhuriyeti şeyhler, dervişler, müritler, meczuplar memleketi olamaz
 En doğru, en hakiki tarikat, medeniyet tarikatıdır En doğru, en hakiki tarikat, medeniyet tarikatıdır |

|
Cevap : Sayısal (Dijital) Elektronik - Sayı Sistemleri |
|
|
#4 |
|
Şengül Şirin

|
Cevap : Sayısal (Dijital) Elektronik - Sayı Sistemleri2  2 2 5 5 3 BİNARY (İKİLİK) SAYILARDA ÇARPMA 3 BİNARY (İKİLİK) SAYILARDA ÇARPMABinary(İkilik) Sayılarla Çarpma işlemi Decimal(Onluk) sayı sisteminin aynısı olup temel çarpma kuralları aşağıdaki gibidir  0 x 0 = 0 0 x 1 = 0 1 x 0 = 0 1 x 1 = 1   2  2 2 5 5 4 BİNARY (İKİLİK) SAYILARDA BÖLME 4 BİNARY (İKİLİK) SAYILARDA BÖLME  2  3 3 OCTAL (SEKİZLİ) SAYI SİSTEMİ OCTAL (SEKİZLİ) SAYI SİSTEMİSayısal Sistemler hernekadar ikilik sayı sistemini kullansalar da bir tasarımcı için Binary (İkilik) sayılarla işlem yapmak zahmetli bir işlem olması nedeniyle farklı sayı sistemlerinin kullanımı tasarımcılar arasında yaygınlaşmıştır  Kullanılan bu sayı sistemlerinden Octal (Sekizli) Sayı sisteminin tabanı sekiz olup 0,1,2,3,4,5,6,7 rakamları bu sayı sisteminde kullanılır Kullanılan bu sayı sistemlerinden Octal (Sekizli) Sayı sisteminin tabanı sekiz olup 0,1,2,3,4,5,6,7 rakamları bu sayı sisteminde kullanılır 2  3 3 1 1 OCTAL(SEKİZLİ) SAYILARIN YAZILIŞI VE DECİMAL(ONLU) SAYILARA ÇEVRİLMESİ OCTAL(SEKİZLİ) SAYILARIN YAZILIŞI VE DECİMAL(ONLU) SAYILARA ÇEVRİLMESİOctal(Sekizli) sayıları Decimal(Onlu) sayılara çevirmek için her sayı bulunduğu basamağın konum ağırlığı ile çarpılır  Bu çarpım sonuçları toplanarak sonuç elde edilir Bu çarpım sonuçları toplanarak sonuç elde edilir  2  3 3 2 2 ONDALIKLI OCTAL(SEKİZLİ) SAYILARIN DECİMAL(ONLUK) SAYILARA ONDALIKLI OCTAL(SEKİZLİ) SAYILARIN DECİMAL(ONLUK) SAYILARAÇEVRİLMESİ Ondalıklı Octal(Sekizli) sayıları Decimal (onluk) sayılara dönüştürmek için izlenilecek yol çarpım 8 metodudur  Ondalıklı kısma kadar olan kısmı normal analiz yöntemini kullanarak dönüştürürken ondalıklı kısmın basamak ağırlığı 0’ı takip eden negatif sayılar olarak belirlenir Ondalıklı kısma kadar olan kısmı normal analiz yöntemini kullanarak dönüştürürken ondalıklı kısmın basamak ağırlığı 0’ı takip eden negatif sayılar olarak belirlenir  2  3 3 3 3 DECİMAL(ONLU) SAYILARIN OCTAL(SEKİZLİ) SAYILARA ÇEVRİLMESİ DECİMAL(ONLU) SAYILARIN OCTAL(SEKİZLİ) SAYILARA ÇEVRİLMESİDecimal(Onluk) sistemden Octal(Sekizli) sisteme dönüşüm “Bölme-8 metodu ile yapılır  Çıkan sonuç tersinden yazılır Çıkan sonuç tersinden yazılır 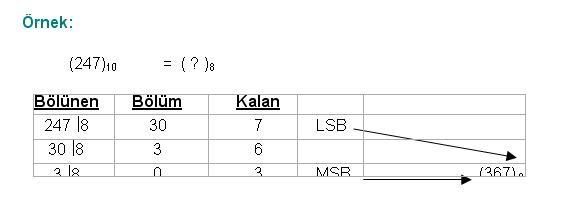 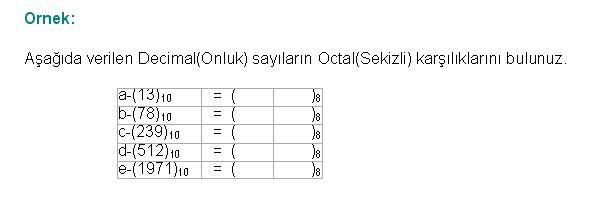 2  3 3 4 4 ONDALIKLI DECİMAL(ONLU) SAYILARIN OCTAL(SEKİZLİ) SAYILARA ONDALIKLI DECİMAL(ONLU) SAYILARIN OCTAL(SEKİZLİ) SAYILARAÇEVRİLMESİ Ondalıklı Decimal(Onlu) Sayıları Octal(Sekizli) sayılara dönüştürürken ondalıklı kısma kadar olan bölüm için normal çevirim yöntemi uygulanır  Ondalıklı kısım ise 8 ile Ondalıklı kısım ise 8 ileçarpılır  Bu işlem kesirli kısım sıfıra veya yakın bir değere ulaşıncaya kadar devam eder Bu işlem kesirli kısım sıfıra veya yakın bir değere ulaşıncaya kadar devam eder 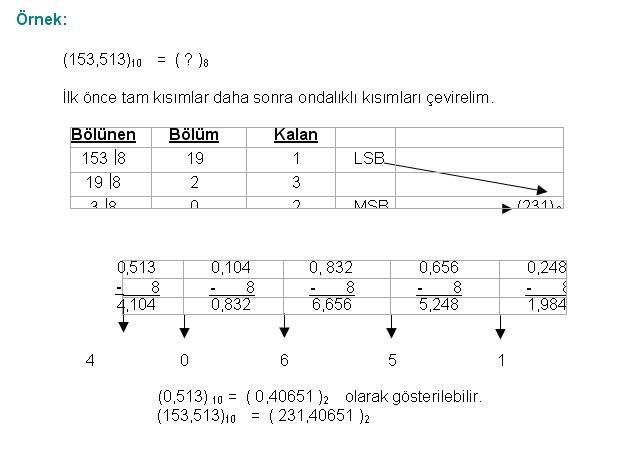  2  3 3 5 5 BİNARY(İKİLİK) SAYILARIN OCTAL(SEKİZLİ) SAYILARA ÇEVRİLMESİ BİNARY(İKİLİK) SAYILARIN OCTAL(SEKİZLİ) SAYILARA ÇEVRİLMESİBinary(İkilik) sayıları Octal(Sekizli) sayılara dönüştürürken,Binary sayı sağdan başlayarak sola doğru üçerli gruplara ayrılır  Her grubun Octal karşılığı bulunarak çevirme işlemi tamamlanmış olur Her grubun Octal karşılığı bulunarak çevirme işlemi tamamlanmış olur 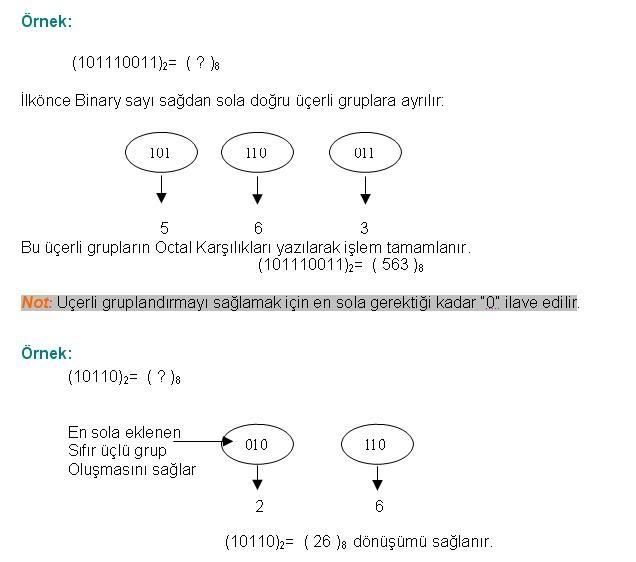 Tam ve kesirli kısmı olan bir Binary sayı halinde tam kısım için,virgülden başlayarak sola doğru, kesirli kısım içinse virgülden başlayarak sağa doğru üçerli gruplar hazırlanır  
__________________
Arkadaşlar, efendiler ve ey millet, iyi biliniz ki, Türkiye Cumhuriyeti şeyhler, dervişler, müritler, meczuplar memleketi olamaz
 En doğru, en hakiki tarikat, medeniyet tarikatıdır En doğru, en hakiki tarikat, medeniyet tarikatıdır |

|
Cevap : Sayısal (Dijital) Elektronik - Sayı Sistemleri |
|
|
#5 |
|
Şengül Şirin

|
Cevap : Sayısal (Dijital) Elektronik - Sayı Sistemleri2  3 3 6 6 OCTAL(SEKİZLİ) SAYILARIN BİNARY(İKİLİK) SAYILARA ÇEVRİLMESİ OCTAL(SEKİZLİ) SAYILARIN BİNARY(İKİLİK) SAYILARA ÇEVRİLMESİOctal (Sekizli) sayıları Binary(İkilik) sayılara ; her Octal (Sekizli) sayının üç bitlik Binary (İkilik) karşılığı yazılması ile çevirim gerçekleştirilir    2  3 3 7 7 OCTAL (SEKİZLİ) SAYI SİSTEMİ ARİTMETİĞİ OCTAL (SEKİZLİ) SAYI SİSTEMİ ARİTMETİĞİ2  3 3 7 7 1 1 OCTAL (SEKİZLİ) SAYILARDA TOPLAMA OCTAL (SEKİZLİ) SAYILARDA TOPLAMADecimal sayı sistemindeki bütün toplama kuralları Octal sayı sisteminde de geçerlidir   2  3 3 7 7 2 OCTAL (SEKİZLİ) SAYILARDA ÇIKARMA 2 OCTAL (SEKİZLİ) SAYILARDA ÇIKARMADecimal sayı sistemindeki bütün çıkarma kuralları Octal sayı sisteminde geçerlidir   2  4 4 HEXADECIMAL (ONALTILI) SAYI SİSTEMİ HEXADECIMAL (ONALTILI) SAYI SİSTEMİHexadecimal (Onaltılık) sayı sisteminin tabanı 16 olup,0-9’a kadar rakamlar ve A-F’ ye kadar harfler bu sayı sisteminde tanımlıdır  Bu sayı sisteminde rakamlar bu sembollerin yan yana yazılmasından elde edilir Bu sayı sisteminde rakamlar bu sembollerin yan yana yazılmasından elde edilir Hanelerin basamak ağırlıkları sağdan sola doğru 16’nın artan kuvvetleri belirtilir Hanelerin basamak ağırlıkları sağdan sola doğru 16’nın artan kuvvetleri belirtilir Aşağıdaki tablo 0-15 arası Decimal(Onlu) sayıların Hexadecimal karşılıklarını vermektedir Aşağıdaki tablo 0-15 arası Decimal(Onlu) sayıların Hexadecimal karşılıklarını vermektedir 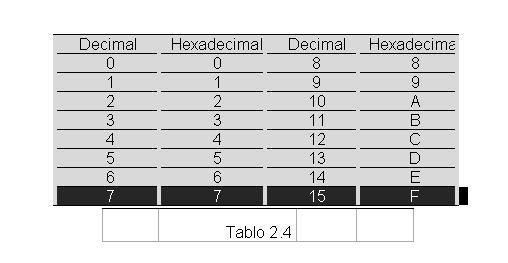 2  4 4 1 1 HEXADECİMAL (ONALTILIK) SAYILARIN YAZILIŞI VE DECİMAL(ONLU) HEXADECİMAL (ONALTILIK) SAYILARIN YAZILIŞI VE DECİMAL(ONLU)SAYILARA ÇEVRİLMESİ Hexadecimal (Onaltılık) sayıları Decimal(Onlu) sayılara çevirmek için her sayı bulunduğu basamağın konum ağırlığı ile çarpılır  Bu çarpım sonuçları toplanarak sonuç elde edilir Bu çarpım sonuçları toplanarak sonuç elde edilir  2  5 5 2 2 ONDALIKLI HEXADECİMAL(ONALTILIK) SAYILARIN DECİMAL(ONLUK) ONDALIKLI HEXADECİMAL(ONALTILIK) SAYILARIN DECİMAL(ONLUK)SAYILARA ÇEVRİLMESİ Ondalıklı Hexadecimal(Onaltılık) sayıları Decimal (onluk) sayılara dönüştürmek için izlenilecek yol “Çarpım 16” metodudur  Ondalıklı kısma kadar olan bölüm normal analiz yöntemini kullanarak dönüştürülürken ondalıklı kısmın basamak ağırlığı 0’ı takip eden negatif sayılar olarak belirlenir Ondalıklı kısma kadar olan bölüm normal analiz yöntemini kullanarak dönüştürülürken ondalıklı kısmın basamak ağırlığı 0’ı takip eden negatif sayılar olarak belirlenir Örnek: ( A,3 )16 = (?)10 dönüşümünü gerçekleştirin? ( A,3 )16 = Ax16º+3x16¹ ( A,3 )16 = 10x1+3x0,0625 ( A,3 )16 = 10+0,1875 ( A,3 )16 = (10,1875)10 2  5 5 3 3 DECİMAL(ONLU) SAYILARIN HEXADECİMAL(ONALTILIK) SAYILARA DECİMAL(ONLU) SAYILARIN HEXADECİMAL(ONALTILIK) SAYILARAÇEVRİLMESİ Decimal(Onlu) sistemden Hexadecimal(Onaltılık) sisteme dönüşüm “Bölme-16 metodu ile yapılır  Çıkan sonuç tersinden yazılır Çıkan sonuç tersinden yazılır  2  5 5 4 4 ONDALIKLI DECİMAL(ONLU) SAYILARIN HEXADECİMAL(ONALTILIK) ONDALIKLI DECİMAL(ONLU) SAYILARIN HEXADECİMAL(ONALTILIK)SAYILARA ÇEVRİLMESİ Ondalıklı Decimal(Onlu) Sayıları Hexadecimal(Onaltılık) sayılara dönüştürürken ondalıklı kısma kadar olan bölüm için normal çevirim yöntemi uygulanır  Ondalıklı kısım ise 16 ile çarpılır Ondalıklı kısım ise 16 ile çarpılır Bu işlem kesirli kısım sıfıra veya sıfıra en yakın değere ulaşıncaya kadar devam eder Bu işlem kesirli kısım sıfıra veya sıfıra en yakın değere ulaşıncaya kadar devam eder  2  5 5 5 5 BİNARY(İKİLİK) SAYILARIN HEXADECİMAL(ONALTILIK) SAYILARA BİNARY(İKİLİK) SAYILARIN HEXADECİMAL(ONALTILIK) SAYILARAÇEVRİLMESİ Binary(İkilik) sayıları Hexadecimal(Onaltılık) sayılara dönüştürürken,Binary sayı sağdan başlayarak sola doğru dörderli gruplara ayrılır  Her grubun Hexadecimal karşılığı bulunarak çevirme işlemi tamamlanmış olur Her grubun Hexadecimal karşılığı bulunarak çevirme işlemi tamamlanmış olur 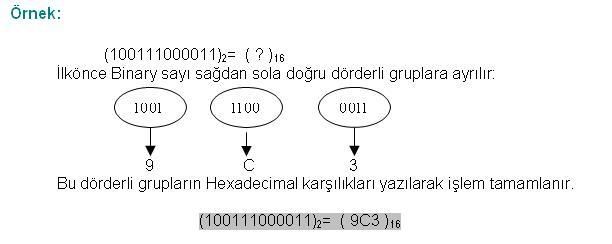 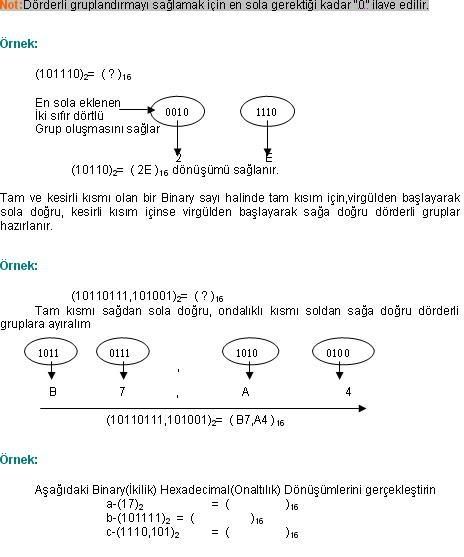 2  5 5 6 6 HEXADECİMAL(ONALTILI) SAYILARIN BİNARY(İKİLİK) SAYILARA HEXADECİMAL(ONALTILI) SAYILARIN BİNARY(İKİLİK) SAYILARAÇEVRİLMESİ Hexadecimal (Onaltılı) sayıları Binary(İkilik) sayılara ; her Hexadecimal (Onaltılı) (Sekizli) sayının dört bitlik Binary (İkilik) karşılığı yazılması ile çevirim gerçekleştirilir   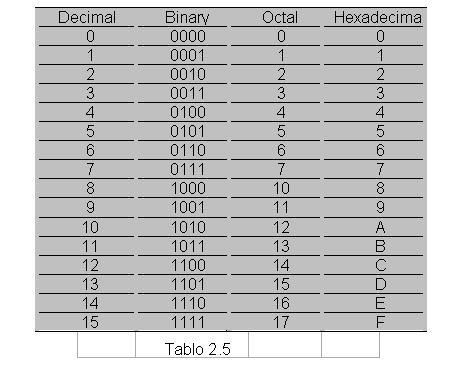 2  5 5 7 7 HEXADECİMAL (ONALTILIK) SAYI SİSTEMİ ARİTMETİĞİ HEXADECİMAL (ONALTILIK) SAYI SİSTEMİ ARİTMETİĞİ2  5 5 7 7 1HEXADECİMAL (ONALTILIK) SAYILARDA TOPLAMA 1HEXADECİMAL (ONALTILIK) SAYILARDA TOPLAMAHexadecimal sayılarla iki şekilde toplama işlemini gerçekleştirebiliriz  Birinci yöntem sayının direk toplanması, diğer bir yöntem ise Hexadecimal sayının herhangi bir sayı sistemine dönüştürülerekmeden toplama işleminin gerçekleştirilmesi Birinci yöntem sayının direk toplanması, diğer bir yöntem ise Hexadecimal sayının herhangi bir sayı sistemine dönüştürülerekmeden toplama işleminin gerçekleştirilmesi Aşağıdaki örnekte her iki şekilde gösterilmektedir Aşağıdaki örnekte her iki şekilde gösterilmektedir  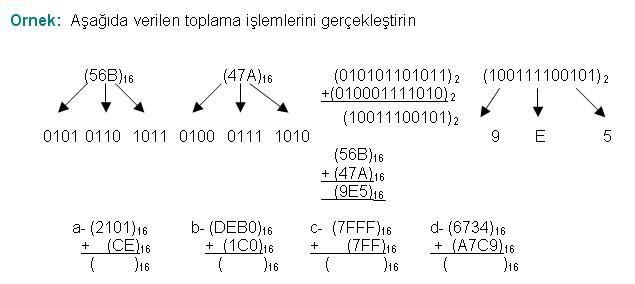 2  5 5 7 7 2 HEXADECİMAL (ONALTILIK) SAYILARDA ÇIKARMA 2 HEXADECİMAL (ONALTILIK) SAYILARDA ÇIKARMATemel çıkarma kuralları geçerli olmak üzere Hexadecimal (Onaltılık) Sayılarla çıkarma işlemi yaparken sayıların direk çıkarılması, Tümleyen aritmetiği gibi yöntemler izlenebileceği gibi bilinen bir sayı sistemine dönüşümü gerçekleştirerek bu sayı sisteminde çıkarma işlemi yapılabilir  
__________________
Arkadaşlar, efendiler ve ey millet, iyi biliniz ki, Türkiye Cumhuriyeti şeyhler, dervişler, müritler, meczuplar memleketi olamaz
 En doğru, en hakiki tarikat, medeniyet tarikatıdır En doğru, en hakiki tarikat, medeniyet tarikatıdır |

|
Cevap : Sayısal (Dijital) Elektronik - Sayı Sistemleri |
|
|
#6 |
|
Şengül Şirin

|
Cevap : Sayısal (Dijital) Elektronik - Sayı SistemleriTümleyen (komplementer) (Tümleyen) Yöntemi İle Hexadecimal Sayıların Çıkarılması Hexadecimal sayılar 15  ve 16 ve 16 olmak üzere iki adet tümleyen (komplementer)e sahiptir olmak üzere iki adet tümleyen (komplementer)e sahiptir Bu iki Tümleyen (komplementer) yardımı ile çıkarma işlemi gerçekleştirmek için ; Bu iki Tümleyen (komplementer) yardımı ile çıkarma işlemi gerçekleştirmek için ;1) Hexadecimal Sayının 15  Tümleyen (komplementer)i her basamağın “ F”sayısından çıkarılması ile bulunur Tümleyen (komplementer)i her basamağın “ F”sayısından çıkarılması ile bulunur 2) Hexadecimal Sayının 16  Tümleyen (komplementer)i 15 Tümleyen (komplementer)i 15 Tümleyen Tümleyen(komplementer)e 1 eklenerek bulunur  şeklinde Hexadecimal sayıların Komplementeleri bulunur  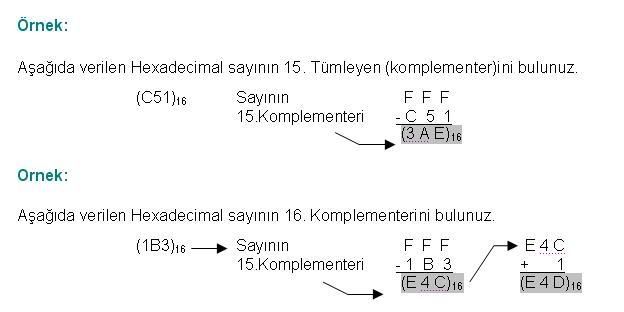 Hexadecimal (Onaltılık) sayıları Tümleyen yardımıyla çıkarmak için; 1) Çıkan sayının 15  veya 16 veya 16 Tümleyen (komplementer)i bulunur Tümleyen (komplementer)i bulunur 2) Ana sayı ile çıkan sayının15  veya 16 veya 16 Tümleyen (komplementer)i toplanır Tümleyen (komplementer)i toplanır 3) Toplam sonunda bir elde oluşmuşsa sonuç pozitiftir; a) İşlem 15  Tümleyen (komplementer) yardımı ile yapılıyorsa oluşan elde en sağdaki basamak ile toplanarak gerçek sonuca ulaşılır Tümleyen (komplementer) yardımı ile yapılıyorsa oluşan elde en sağdaki basamak ile toplanarak gerçek sonuca ulaşılır b) İşlem 16  Tümleyen (komplementer) yardımı ile yapılıyorsa oluşan bu elde dikkate alınmaz Tümleyen (komplementer) yardımı ile yapılıyorsa oluşan bu elde dikkate alınmaz 4- Toplam sonunda bir elde oluşmamışsa sonuç negatiftir; a) İşlem 15  Tümleyen (komplementer) yardımı ile yapılıyorsa gerçek sonuç toplam sonucunun 15 Tümleyen (komplementer) yardımı ile yapılıyorsa gerçek sonuç toplam sonucunun 15 Tümleyen (komplementer)idir Tümleyen (komplementer)idir b) İşlem 16  Tümleyen (komplementer) yardımı ile yapılıyorsa gerçek sonuç toplam sonucunun 16 Tümleyen (komplementer) yardımı ile yapılıyorsa gerçek sonuç toplam sonucunun 16 Tümleyen (komplementer)dir Tümleyen (komplementer)dir 
__________________
Arkadaşlar, efendiler ve ey millet, iyi biliniz ki, Türkiye Cumhuriyeti şeyhler, dervişler, müritler, meczuplar memleketi olamaz
 En doğru, en hakiki tarikat, medeniyet tarikatıdır En doğru, en hakiki tarikat, medeniyet tarikatıdır |

|
Üye olmanıza kesinlikle gerek yok !
Konuya yorum yazmak için sadece buraya tıklayınız.
Bu sitede 1 günde 10.000 kişiye sesinizi duyurma fırsatınız var.
IP adresleri kayıt altında tutulmaktadır. Aşağılama, hakaret, küfür vb. kötü içerikli mesaj yazan şahıslar IP adreslerinden tespit edilerek haklarında suç duyurusunda bulunulabilir.
Konuya yorum yazmak için sadece buraya tıklayınız.
Bu sitede 1 günde 10.000 kişiye sesinizi duyurma fırsatınız var.
IP adresleri kayıt altında tutulmaktadır. Aşağılama, hakaret, küfür vb. kötü içerikli mesaj yazan şahıslar IP adreslerinden tespit edilerek haklarında suç duyurusunda bulunulabilir.
«
Önceki Konu
|
Sonraki Konu
»
|
|
ForumSinsi.com hakkında yapılacak tüm şikayetlerde ilgili adresimizle iletişime geçilmesi halinde kanunlar ve yönetmelikler çerçevesinde en geç 1 (Bir) Hafta içerisinde gereken işlemler yapılacaktır. İletişime geçmek için buraya tıklayınız.



