Matematikçiler /Pierre De Fermat

Pierre de Fermat


Pierre de Fermat


Pierre de Fermat (piyer dö ferma okunur) (d 1601, Beaumont-de-Lomagne – ö 12 Ocak 1665, Castres), Bask kökenli Fransız hukukçu ve matematikçi İlk öğrenimini doğduğu şehirde yapmıştır Yargıç olmak için çalışmalarına Toulouse’de devam etmiştir Fermat, memurluğunun yoğun işlerinden geriye kalan zamanlarında matematikle uğraşmıştır Arşimet'in eğildiği diferansiyel hesaba geometrik görünümle yaklaşmıştır Sayılar teorisinde önemli sonuçlar bulmuş, olasılık ve analitik geometriye de katkılarda bulunmuştur
Günümüzde hatırlanmasının en önemli sebebi Fermat'nın Son Teoremi'dir Modern sayılar kuramının kurucusu olarak kabul edilen 17 yüzyıl matematikçisi Pierre de Fermat'nın adını taşıyan bu teorem, şu şekilde ifade edilebilir:
Herhangi x, y, ve z pozitif tam sayıları için,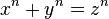
ifadesini sağlayan ve 2'den büyük bir doğal sayı n yoktur Fermat, bu problemi çözmüş, kanıtı da Eski Yunanlı matematikçi Diaphontos'un Arithmetika adlı kitabının kendindeki kopyasının sayfalarından birinin kenarına 1637'de şöyle yazmıştı:

x, y, z ve n pozitif tamsayılar ve n>2 olmak koşuluyla, x^n + y^n = z^n denkleminin çözümü yoktur Ben bunun kanıtını buldum, ama kanıtı bu kenar boşluğuna sığdırmak olanaksız

Ancak bu kanıt bulunamamıştır Fermat'tan sonra matematikçiler bu önermenin bir türlü içinden çıkamamışlardır Fermat'ın bıraktığı defterler arasında teoremin kanıtına rastlayamadıkları gibi, kendileri de ne doğruluğunu ne yanlışlığını kanıtlayabilmişlerdir Yıllar boyunca (300 yıl sonrasına kadar) bu konuda yapılan çalışmalar sonucu bu teoremin Shimura-Taniyama Konjektürü'nün bir özel durumu olduğu anlaşılmış, ardından da 1993'te İngiliz matematikçi Andrew Wiles, eski öğrencilerinden Richard Taylor'ın da yardımıyla ve cebirsel geometrinin çok karmaşık araçlarını kullanarak teoremi kanıtlamanın bir yolunu bulmuş ve bu kanıtı 1995'te Annals of Mathematics adlı dergide yayımlamıştır Shimura-Taniyama Konjektürü'nün böylelikle ispatlanması sonucu Fermat'nın Son Teoremi de 1995'te ispatlanmış oldu
Asal sayılar üzerinde çok durmuştur Onun bu konuda çeşitli teoremleri vardır Örneğin,
4n + 1 şeklinde yazılan bir asal sayı p, yalnızca bir tek şekilde iki karenin toplamı olarak yazılabilir
Mesela en ufak asal sayılar p:
5 = 12 + 22 ve 13 = 22 + 32 dir Bu teoremi daha sonra Euler kanıtlamıştır

F ermat (1601-1665), modern sayılar teorisinin kurucusudur Onun bu konuda çeşitli teoremleri vardır Örneğin, (4n + 1) şeklinde yazılan bir asal sayı, yalnızca bir tek şekilde iki karenin toplamı olarak yazılabilir Bu teoremi daha sonra Euler kanıtlamıştır "Fermat Teoremi" olarak tanınan meşhur teoremi ise, "P asal bir sayı ve a ile P aralarında asal olduğu zaman, (ap-1 - 1) sayısı P sayısına bölünebilir" biçiminde ifâde edilebilir Bu teoremi Leibniz ve Euler ispatlamışlardır Fermat ayrıca x2 - Ay2 = 1 denkleminin (A kare olmayan bir tam sayıdır) sınırsız sayıda tam sayılı çözümü bulunduğunu görmüştür

Fermat'nın asıl önemli teoremi ise, "xn + yn = zn denklemi x, y, z ve n'nin pozitif değerleri için eğer n>2 ise imkânsızdır" biçimindedir Bütün n'ler için doğru olan kanıt henüz bulunmamıştır, ama teorem çok sayıda değer için doğrudur

Fermat, bütün teoremlerinin dakik ispatlarını vermemişti 1879 yılına kadar onun kullanmış olduğu ispat yöntemleri tamamıyla kayıptı; bu tarihte Leiden Kütüphanesi'nde Huygens'in yazmaları arasında bulunan bir belge, Fermat'nın indüktif metodu kullandığını gösterdi Fermat, bu metodun, özellikle belirli bağıntıların imkânsızlığının ispatına uygun olduğunu söylemiştir

Fermat matematiksel olasılıklar kuramının da kurucusuydu Pascal ile birlikte, bir şans oyununda her oyuncunun kazanma olasılığı problemi üzerinde durmuş ve kombinasyonlar teorisiyle problemi çözmüştür