 07-11-2009
07-11-2009
|
#2
|
Şengül Şirin
|

Cevap : Sayısal (Dijital) Elektronik - Sayı Sistemleri
2 2 2 BİNARY (İKİLİK) SAYI SİSTEMİ Binary (İkilik) Sayı sisteminin tabanı 2’dir BİNARY (İKİLİK) SAYI SİSTEMİ Binary (İkilik) Sayı sisteminin tabanı 2’dir Ve bu sistemde sadece “0” ve “1” rakamları kullanılmaktadır Ve bu sistemde sadece “0” ve “1” rakamları kullanılmaktadır Binary Sayı sisteminde’ de Decimal(Onlu) Sayı sisteminde olduğu gibi her sayı bulunduğu basamağın konum ağırlığı ile çarpılır Binary Sayı sisteminde’ de Decimal(Onlu) Sayı sisteminde olduğu gibi her sayı bulunduğu basamağın konum ağırlığı ile çarpılır
Binary(İkilik) Sayı Sisteminde bulunan her ‘0’ veya ‘1’ rakamları BİT (BInary DigiT)
adı ile tanımlanır Binary(İkili) sayılar yazılırken en sağdaki basamağa en düşük değerlikli bit (Least Significant Bit-LSB),en soldaki basamağa en yüksek değerlikli bit Binary(İkili) sayılar yazılırken en sağdaki basamağa en düşük değerlikli bit (Least Significant Bit-LSB),en soldaki basamağa en yüksek değerlikli bit
(Most Significant Bit-MSB) adı verilir
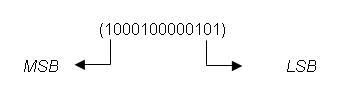
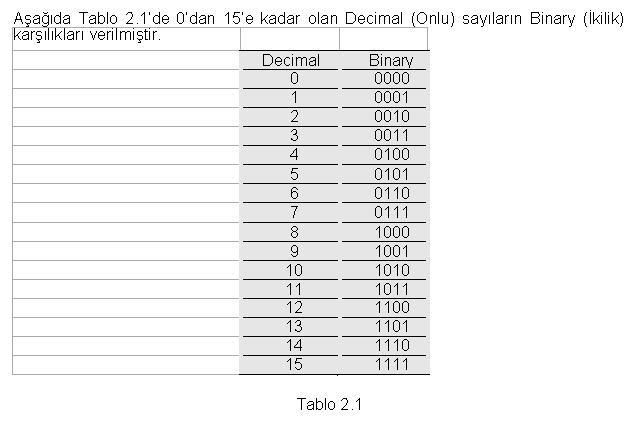
Decimal(Onlu) Sayılıları sadece iki rakamdan oluşan Binary(İkilik) sayılarla tanımlayabilmemiz Sayısal Sistemlerin iki voltaj seviyesini kullanarak farklı büyüklükleri tanımlanmasının anlaşılmasını sağlamaktadır
2 2 2 1 1 BİNARY SAYILARIN YAZILIŞI VE DECİMAL SAYILARA ÇEVRİLMESİ BİNARY SAYILARIN YAZILIŞI VE DECİMAL SAYILARA ÇEVRİLMESİ
Binary sayıların yazımında tabanın iki olduğu unutulmamalıdır Binary(ikili) sayıları Decimal(Onlu) sayılara dönüştürürken her bir bit basamak ağırlığı ile çarpılıp bu sonuçların toplanması gerekir Binary(ikili) sayıları Decimal(Onlu) sayılara dönüştürürken her bir bit basamak ağırlığı ile çarpılıp bu sonuçların toplanması gerekir

Birkaç örnekle hem Binary sayıların yazımını ve Decimal(Onlu) sayılara dönüşümünü
inceleyelim
Örnek:
(1010)2 = ( ? )10
(1010)2 = 1 x 23 + 0 x 22 + 1 x 21 + 0 x 20
(1010)2 = 8 + 0 + 2 + 0
(1010)2 = 10
Örnek:
(11001)2 = ( ? )10
(11001)2 = 1x 24+1x 23+0x 22+0x 21+1x 20
(11001)2 = 16 + 8 + 0 + 0 + 1
(11001)2 = 25
Not:
Binary (İkilik) sayıların Decimal(Onlu) karşılıkları bulunurken her basamak kendi
basamak ağırlığı ile çarpılır Çarpım sonuçları toplanarak dönüşüm tamamlanır Çarpım sonuçları toplanarak dönüşüm tamamlanır
Örnek:
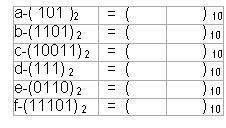
Aşağıda verilen Binary(İkilik) sayıların Decimal(Onlu) (Onlu ) karşılıklarını bulunuz
2 2 2 2 2 ONDALIKLI BİNARY SAYILARIN DECİMAL SAYILARA DÖNÜŞTÜRÜLMESİ ONDALIKLI BİNARY SAYILARIN DECİMAL SAYILARA DÖNÜŞTÜRÜLMESİ
Ondalıklı Binary (ikilik) sayıları Decimal (onlu) sayılara dönüştürmek için izlenilecek yol çarpım iki metodudur Ondalıklı kısma kadar olan kısmı normal analiz yöntemini kullanarak dönüştürürken ondalıklı kısmın basamak ağırlığı 0’ı takip eden negatif Ondalıklı kısma kadar olan kısmı normal analiz yöntemini kullanarak dönüştürürken ondalıklı kısmın basamak ağırlığı 0’ı takip eden negatif
sayılar olarak belirlenir
Örnek:
( 111,101 )2 = (?)10
( 111,101 )2 = 1x2²+1x2¹+1x2º+1x2¯¹+0x2¯²+1x2¯³
( 111,101 )2 = 1x4+1x2+1x1+1x½+0x¼+1x⅛
( 111,101 )2 = 4+2+1+0,5+0+0,125
( 111,101 )2 = (7,625)10
Örnek:
Aşağıda verilen Ondalıklı Binary (İkilik) sayıların Decimal(Onlu) karşılıklarını bulunuz
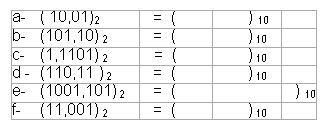
2 2 2 3 3 DECİMAL SAYILARIN BİNARY SAYILARA ÇEVRİLMESİ DECİMAL SAYILARIN BİNARY SAYILARA ÇEVRİLMESİ
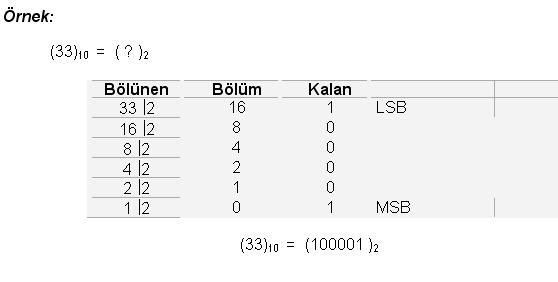
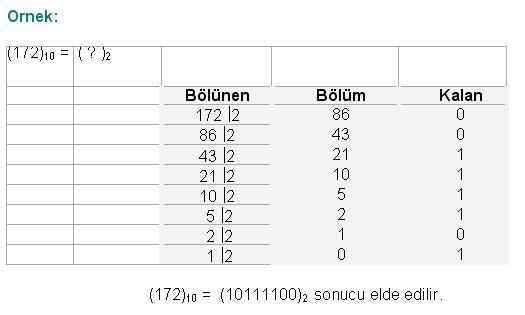
Decimal(Onlu) sayıları Binary(İkilik) sayılara çevirirken “Bölme-2” metodu kullanılır Çıkan sonuç tersinden yazılır Çıkan sonuç tersinden yazılır
İkili sayı sistemi, sayısal sistemlerin bilgiyi tanımlayabilmesi için yeterli olmasına rağmen fazla sayıda basamak kullanılması, bu sayı sistemi ile ilgili işlemlerin çok uzun sürmesi hata olasılığını beraberinde getirmektedir 
2 2 2 4 4 ONDALIKLI DECİMAL SAYILARIN BİNARY SAYILARA ONDALIKLI DECİMAL SAYILARIN BİNARY SAYILARA
DÖNÜŞTÜRÜLMESİ
Ondalıklı Decimal(Onlu) Sayıların Binary(İkilik) karşılıkları bulunurken ondalıklı kısma kadar olan bölüm için normal çevirim yöntemi uygulanır Ondalıklı kısım, kesirli kısmın sıfıra veya sıfıra yakın bir değere ulaşıncaya kadar 2 ile çarpılır Ondalıklı kısım, kesirli kısmın sıfıra veya sıfıra yakın bir değere ulaşıncaya kadar 2 ile çarpılır
Örnek:
(7,8125)10 = ( ? )2
ondalıklı decimal(onluk) sayısının binary(ikilik) karşılığını yazınız

Örnek:
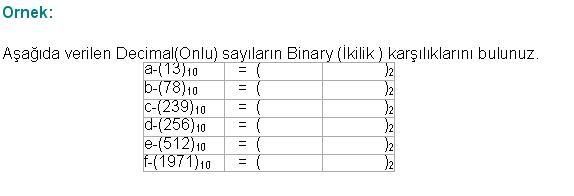
Aşağıdaki Ondalıklı Decimal sayıları Binary Sayılara dönüştürün;
a-(0,125)10 = ( ? )2 b-(11,1451)10 = ( ? )2 c-(125,65)10 = ( ? )2
2 2 2 5 5 BİNARY SAYI SİSTEMİ ARİTMETİĞİ BİNARY SAYI SİSTEMİ ARİTMETİĞİ
2 2 2 5 5 1 1 BİNARY SAYILARDA TOPLAMA BİNARY SAYILARDA TOPLAMA
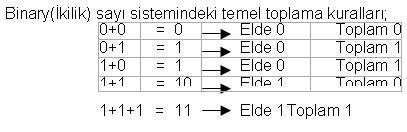
şeklinde belirtilebilir Binary sayı sisteminde de iki sayı toplandığında eğer sonuç bir haneye sığmıyorsa bir elde(cary) oluşur Binary sayı sisteminde de iki sayı toplandığında eğer sonuç bir haneye sığmıyorsa bir elde(cary) oluşur

En sağdaki sütun 1 + 1 = 0 1 oluşan elde bir üst basamakla
toplanır
Ortadaki sütün 1 + 1 + 0 = 0 1 oluşan elde bir üst basamakla toplanır
En soldaki sütun 1 +0 + 0 = 1 0
Not:
Eğer en yüksek değerlikli basamakların toplamında bir elde oluşmuş olsaydı, bu
toplam sonucunun en yüksek değerlikli biti olarak karşımıza çıkardı

__________________
Arkadaşlar, efendiler ve ey millet, iyi biliniz ki, Türkiye Cumhuriyeti şeyhler, dervişler, müritler, meczuplar memleketi olamaz En doğru, en hakiki tarikat, medeniyet tarikatıdır En doğru, en hakiki tarikat, medeniyet tarikatıdır
|
|
|

|