Fizik - Düzgün Dairesel Hareket

Sabit bir kuvvet, büyüklüğü değişmeyen hız vektörüne sürekli ve dik olarak etki ederse, cisme, R yarıçaplı çember üzerinde düzgün dönme hareketi yaptırır Böyle bir hareket düzgün dairesel harekettir

Periyot ve Frekans

Periyot

Düzgün dairesel harekette bir tam dolanım için geçen süredir T ile gösterilir Birimi saniyedir

Frekans

Düzgün dairesel hareket yapan cismin bir saniyedeki dolanım sayısıdır f ile gösterilir Birimi Hertz dir

Periyot ve frekans arasında, bağıntısı vardır

Hız


Şekil 1


Çember üzerinde dolanan bir cisim, Şekil 1 deki gibi x kadar yol alırken yarıçap vektörü aynı anda θ açısı kadar bir açı tarar Bu nedenle dairesel hareketlerde; biri çizgisel, diğeri açısal olmak üzere iki çeşit hız tanımlanır

Çizgisel Hız


Şekil 2


Şekil 2 deki gibi düzgün dairesel hareket yapan bir cismin, daire yayı üzerinde birim zamanda aldığı yola çizgisel hız denir Çizgisel hız vektörü () daire yayına tam teğet olup, yarıçap vektörüne diktir


Düzgün doğrusal harekette; (veya ) idi Cisim dairenin tüm çevresini dolanırsa, 2πr kadar yol alır ve bu esnada bir periyot (T) kadar zaman geçer
Bu nedenle çizgisel hız ifadesi;


şeklinde bulunur Çizgisel hızın birimi metre / saniye dir

Açısal Hız

Cismi merkeze bağlayan yarıçap vektörünün, birim zamanda radyan cinsinden taradığı açıya açısal hız denir ω ile gösterilir Birimi rad/s dir
Dairesel hareket yapan bir cismi merkeze bağlayan yarıçap vektörü bir tam devir yaptığında, 2π radyan açı tarar ve bu esnada bir periyot (T) kadar zaman geçer O hâlde açısal hız;
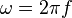
olur Çizgisel hız ile açısal hız arasındaki bağıntı ise;
olmak üzere olur

İvme ve Kuvvet

Merkezcil İvme


Şekil 3


Dairesel bir yörüngede sabit hızla dönen bir cismin, eşit zaman aralıklarıyla çizilmiş hız vektörleri Şekil 3 teki gibi olur Bu hız vektörlerinin büyüklükleri eşit, yönleri ise farklıdır
Hız vektörlerinin başlangıç noktaları ortak bir noktada toplanırsa ardışık hız değişim vektörlerinin eşit büyüklükte, fakat farklı yönlerde olduğu görülür Δt süresindeki hız değişim vektörü ise, ortalama ivme vektörü;
olur Ani ivme vektörleri, hız vektörlerine diktir
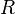
Düzgün dairesel hareket yapan bir cisim, yarıçaplı çember üzerinde bir devir yaptığında, hız vektörü de tam bir devir yaparak başlangıçtaki yönüne gelir Diğer bir deyişle, hız vektörünün ucu, r yarıçaplı bir dairenin 2πr çevresini zamanda döner Hızdaki değişim; Δv = 2πr olduğundan;


olur Çizgisel hızın değeri ivme bağıntısında yerine yazılırsa;


veya bulunur
Dairesel harekette bu ivmeye merkezcil ivme denir



Şekil 4


Buradaki ( − ) işareti vektörüyle ivme vektörünün aynı doğrultuda ve ters yönlü olduğunu gösterir (Şekil 4)

Merkezcil Kuvvet

Her ivme, kendi yönünde bir net kuvvet tarafından oluşturulur Düzgün dairesel harekette de cisme ivme kazandıran kuvvet dinamiğin temel prensibi olan dan;


dir Bu kuvvetin yönü, ivme ile aynı yönlü olup yörüngenin merkezine doğrudur Bu kuvvete merkezcil kuvvet denir Kuvvetin büyüklüğü, v hızı ile R yarıçapına bağlı olarak;


şeklinde de yazılabilir


Merkezkaç Kuvveti


Şekil 5


Dairesel harekette merkezkaç kuvveti adı verilen bir kuvvet daha vardır Newton yasalarının geçerli olduğu bir referans sisteminde böyle bir kuvvet yoktur Bu kuvvetin çıkma sebebi gözlemcinin sistemde Newton yasalarını uygulayabilmek için varsaydığı eylemsizlik kuvvetidir (Şekil 5)
Vikipedi